13장/Introduction to Analysis Of Variance(ANOVA)

13.1 Introduction

13.2 Logic of Analysis of Variance

13.3 ANOVA Notation and Formulas

13.4 Distribution of F - Ratios

13.5 Examples of Hypothesis Testing and Effect Size with ANOVA

13.6 Post Hoc Tests

 

 

- analysis of variance (anova)

 

t 검정은 오직 두개의 그룹을 비교하는 것에 한정되어있었다.

 

-아노바

factor : 비교되는 그룹을 지정하는 변수

 

compared (e.g.: temperature, age)

 

level : 독립적인 조건과 값이고 그것이 factor를 구성하는 것이다. 

(e.g.: three levels of temperature, three levels of age)

 

 

평균 차이가 있는지 계산해라....

 

3개의 다른 기온 조건이 있을 때 학습의 퍼포먼스를 평가: 50도 70도 90도

 

영가설 : 온도는 퍼포먼스에 영향을 주지 않는다.

 

대립가설 : 온도는 학습 효과에 영향을 준다.

최소한 하나의 모집단 평균이 다른 것들과 다를 때

 

anova의 검정 방법은 t 방법과 유사하다.

 

t에서는 비율을 계산했다. -> 샘플 평균 사이의 주어진 차이 / 우연에 의한 차이 (error)

 

아노바에서 테스트는 f-ratio를 사용한다.

f=variance(diffrences) between sample means/ variance(differences) expected by chance(error)

 

f-ratio는 분산을 기반으로 한다 (샘플평균의 차이 대신에)

그 이유는 anova는 보통 두 샘플 평균 이상이 존재한 상황에서 사용하기 때문에 

 

-만약 두개 샘플 이상이 존재한다면 샘플의 평균 차이를 구하기는 불가능함

-f-ratio 의 숫자 내의 분산에서는 모든 샘플 평균 사이의 차이를 설명할 수 있는 하나의 숫자를 제공한다.

 

f-ratio

분자(numerator) : 모든 샘플 평균 사이의 차이 를 설명하는 하나의 값

분모 (denominator) : 우연에 의한 것이나 혹은 샘플 에러의 차이

 

t test :추정된 표준 오차를 사용한다 얼마나 차이가 운에의해 나타내어지는 지를 측정하기 위해

 

anova : 만약 효과가 없다면 얼마나 차이가 큰지를 측정하기 위해 분산을 사용한다.

 

왜 t 검정을 쉽게 복제할 수 없을까?

부풀려진 알파 레벨의 문제를 피하기 위해

 

 

3개의 온도의 조건이 존재할 때 퍼포먼스

 

목표 : 차이의 크기와 그 차이가 어느 곳에서 오는지를 측정하기

 

 

-전체적인 변동성

모든 다른 샘플으로부터 모든 점수들을 합친다. 이것은 하나의 제너럴한 변동성의 측정을 얻기 위해서이다. (완전한 실험을 위해)

 

-그것을 각각의 다른 요소들로 분해해라

-트리트먼트 분산 사이 (–Between-Treatments Variance)

샘플 평균 사이에서 차이를 측정한다.

 

-within - treatment variance

각각의 트리트먼트 조건 내부의 변동성 측정

 

•Between-Treatments Variance

트리트먼트 조건 사이에서 얼마나 차이가 존재하는지 측정한다.

 

1. 트리트먼트 사이의 차이들은 트리트먼트 효과 때문이다.(treatment effects)

2.트리트먼트 사이의 차이는 단순히 운(chance)떄문이다.

(연구원의 어떠한 행위에 의해 예측되지 않은 차이 )

 

문제 : 트리트먼트 효과와 우연의 분산은 섞인것

따라서 트리트먼트 효과 그 자체를 측정한다는 것은 불가능 하다.

 

해결책 : anova에서 chance differences 를 측정함으로써 해결 (우연의 차이를 측정)

구성: within treatments 분산을 계산

 

각각의 트리트먼트 조건 inside 

우리는 각각의 세트를 가진다(정확이 동일하게 다뤄지는)

하지만, 그 각각의 점수는 동일한 트리트먼트 조건에서 다르다..

 

왜 점수가 다른가?

단순이 우연에 의해

각각의 차이와 실험적인 오류 때문에

 

따라서, within-treatments variance 는 우연에 의해서 얼마나 차이가 합당한지에 대한 측정을 제공한다.

트리트먼트 효과가 존재하지 않을 때, within - treatments 분산 측정은 얼마나 큰 차이가 존재하는지 말해줌?

 

 

아노바 - total variability 

between-treatments variance : treatment effec / difference due to chance 

within - treatments variance : differences due to chance

 

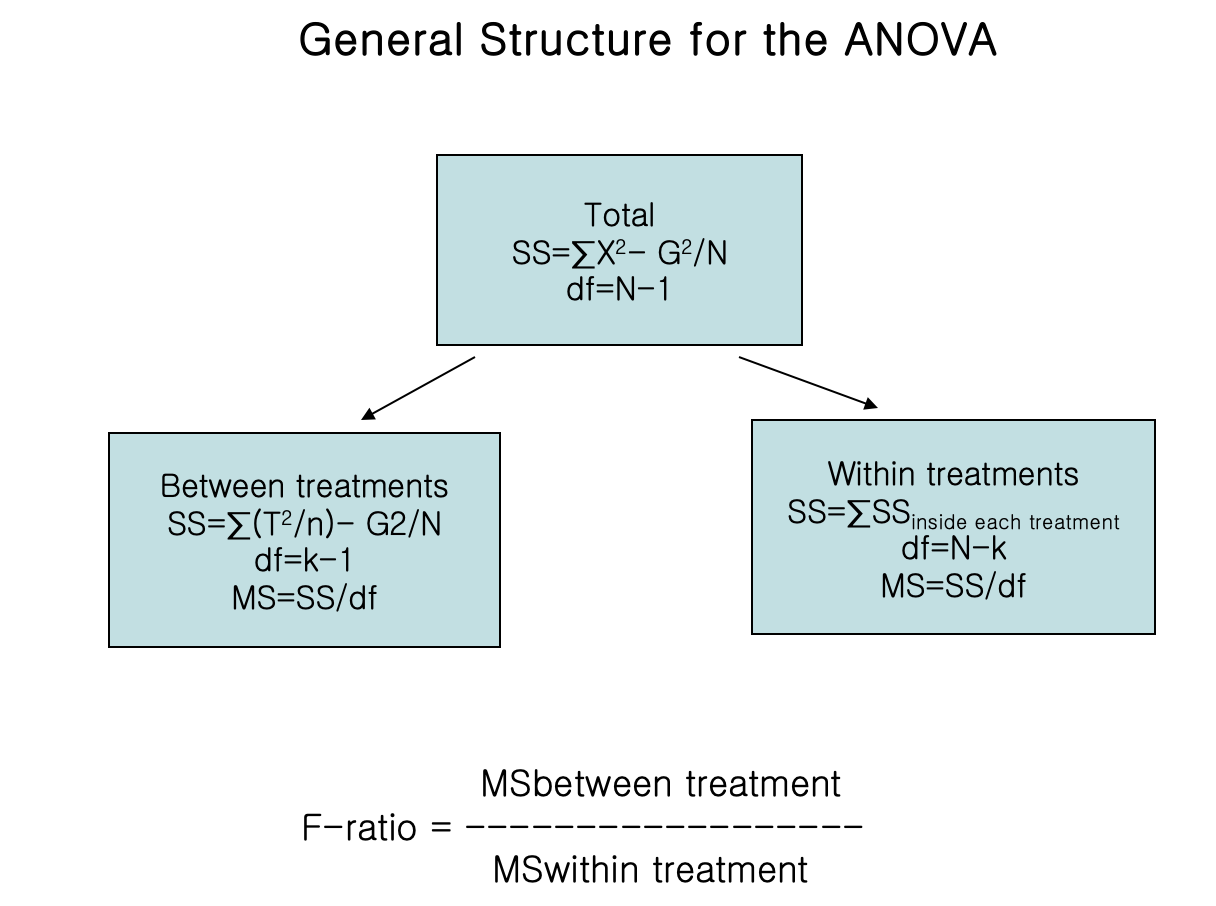
-anova structure 

아노바에 대한  계산의 구조 

 

트리트 먼트사이의 분산 / 트리트먼트 내부의 분산   => f - ratio 를 구하는 목표

 

 

f-ratio내부의 각각의 분산은 ss/df로 나눠진다.

-ss와 df 값을 각각 얻기 위해서는 , 전체적인 변동성이 두개의 요소로 분석된다.

 

-f-ratio: 두개의 기본적인 콤포넌트의 단순한 비교이다 (between / within treatments) 

 

 

f= treatment effect + differences due to chance / differences due to chance

 

f-ratio에서 얻어진 값은 어떤한 효과가 존재했는지 안했는지를 결정하는데에 도움을 줄것임

 

두개의 상황

트리트먼트가 효과가 없을 때(F-ratio ≒ 1)

트리트먼트가 효과가 있을 때 (F-ratio > 1)

 

-anova notation & formulas 

factor : 독립 변수 (ex : temperature)

 

level : 독립적 트리트먼트 조건 -> factor를 구성함 (ex:온도 요인은 3개의 구간으로 구성)

 

 

 

-분산 계산 (calculation of variance) = MS

anova에서 variance용어 대신에 평균 제곱의 용어를 사용하는 것이 관습적이다.(mean square) Ms

-f-ratio

F=MSbetween =MSwithin (ex:15/1.33 = 11.28)

f=11.28 ( f-ratio의 분자는 분모의 수보다 크다) check : spss 

 

트리트먼트 사이의 차이를 나타내는 것은 우연보다크다.

 

-reporting

 

 

-f-ratio의 분산

특성

1) f 값은 항상 positive할 것이다.

2)영가설이 true일 때, f-ratio는 1.00에 가까워진다.

따라서, f-ratio의 분산은 1.00에 쌓이게됨.

 

 

 

 

 

영가설 : 효과없으면 모두 같은 값 

대립가설 : 트리트먼트 평균이 다름

 

기각역 설정

계산

 

 

- 효과 크기 측정 

r^2 결정계수 : 점수 사이의 차이가 얼마나 큰지 측정하기 . 이것은 트리트먼트 사이의 차이에 의해 설명된다.

 

-독립측정 아노바의 전제조건 

1)각각의 샘플에 대한 관측은 독립적이어야한다.

2)샘플이 추출된 모집단은 정규분포를 띄어야한다.

3)모집단은 동일한 분산을 가져야한다.

 

-사후검정

두개의 트리트먼트 케이스

영가설이 기각된다면 두개의 평균은 동일하지 않은 경우임 

 

두개 이상의 트리트먼트 케이스

영가설을 기각한다면 모든 평균이 동일하지 않은 것임

 

->우리는 어느 하나가 다른지 결정해야한다.

 

영가설을 기각 하는 것은 적어도 다른 하나가 존재한다는 것임

 

answer : 사후검정 :어느 평균 차이가 유효한지 아닌지 결정하기 위한 아노바 후에 추가적인 검정

 

일반적인 경우 사후검정 

:데이터를 통해 돌아가고 각각의 트리트먼트를 비교한다. 

–Go back through the data and compare the individual treatments two at a time à pairwise comparisons

 

-다른 가설 검정의 연속을 수행한다.  : 제 1종에러를 모으는 것의 위험

-사후검정 상황에서 1종에러를 컨트롤 하는 방법 : 튜키의 hsd, scheffe test 

 

tukey's hsd

hsd : 진실되게 유의미한 차이

유의미한것을 위해 필요한 트리트먼트 평ㄱㄴ 사이으 ㅣ최소한의 차이를 결정하는 하나의 값을 계산하는 것이다.

 

평균차이가 튜키의 hsd 를 초과하면 우리는 트리트먼트 사이의 유의미한 차이가 존재한다고 가정한다.

 

 

-scheffe test

모든 가능한 사후분석 검정 중에 가장 안전한 것이다. 

scheffe는 모든 사후검정이 완전한 분산 분성을 위해 동일한 기각역을 사용하는 것을 만족할 것을 요구한다.

 

1)오직 두개의 트리트먼트만 비교할 때 , scheffe 시험은 오리지널 실험으로부터의 k의 값을 이용한다. 이것은 df.between tretment를 계산하기 위함이다.

 

2)scheffe는 모든 사후 분석이 완전한 분산 분석을 위해 동일한 기각역을 사용할 것을 요구한다.

-아노바와 t test사이의 관계

 

우리가 독립측적연구로부터 데이터를 가질때 오직 두개의 트리트먼트 조건과 함께

- 우리는 t test 혹은 독립적인 측적 아노바를 사용한다.

 

t 통계값과 f-ratios 사이에서 기초적인 관계는

F=t^2

t 통계는 차이를 기반으로 하고 f-ratio는 제곱의 차이를 기반으로 하기 때문에