ch.10 The t-Test for Two Independent Samples

10.1 Overview

10.2 The t Statistic for an Independent-Measures Research Design

10.3 Hypothesis Tests and Effect Size with the Independent-Measures t Statistic

10.4 Directional Tests and Assumptions for the Independent-measures t

 

 

지금까지 모집단에 대해 하나의 샘플의 결론을 내는 것에 대해 배웠고,

많은 조사들이 두개의 데이터 비교를 요구하는 경우가 많다.

 

두개의 데이터 셋은 완전히 다른 샘플에서 오는 경우가 많다(ex: 남성 여성)

 

-두개의 샘플이 있는 경우 : first sample (n1,m1) / second sample(n2,m2)

 

목적 & 가정

두개의 모집단사이의 평균을 계산하기

 

–H0: μ1 -  μ2 = 0 (no difference between the population means) -> 평균이 같으므로 차이 x

 

–H1: μ1 -  μ2 ≠ 0 (there is mean difference between the populations) -> 평균이 다르므로 차이 x

 

-하나의 샘플의 티 값

 

–t = (M – μ)/sM   (샘플 평균 - 모집단 평균) / 추정된 표준 오차

 

-두개의 샘플의 티 값

 

두개의 샘플 평균을 사용한다. 이것은 두개의 모집단 평균에 대한 가정이다.

–t = [(M1 - M2) – (μ1 - μ2)]/ s(M1-M2)

 

= (sample mean difference – population mean difference) / estimated standard error

 

    = sample mean difference / estimated standard error (since H0 sets the population mean difference is zero)

  t = (M1 - M2) / s(M1-M2) -> 모집단의 평균 차이가 0이기 때문에 )?????

 

-t에서의 표준 오차 

티 공식에서의  표준 오차는 얼마나 샘플의 통계가 모집단의 파라미터를 잘 설명하느냐를 보여준다.

 

하나의 샘플 (se)

샘플 평균에 대한 측정된 에러값?

 

두개의 샘플에러 (sm1-m2)

모집단의 평균 차이를 보여주기 위해서 샘플의 평균차이를 사용할때 기대되는 에러의 양을 측정한다.

 

 

-pooled variance(합동 분산)

샘플에 대한 분산 

-하나의 t 통계값

•s2 = SS/df

 

독립적인 측정(두개의 값?)

•s2p = (SS1 + SS2)/(df1 + df2)

 

두개의 샘플으로부터의 값은 합동분산을 계산하기 위해 합쳐진다.

 

합동분산은 두개의 샘플 분산의 평균이다.

 

 

 

-Estimated Standard Error

•One-sample SE = sM =√s2 /n  -> 샘플 평균 M이 모집단의 평균 u를 얼마나 정확하게 측정하는지 나타냄

 

two-sample SE=s(M1-M2) =√(s2p /n1)+ (s2p /n2)

 

->두개의 샘플평균사이에서 두개의 모집단 평균사이의 차이를 얼마나 잘 차이를 보여주는지 츠겆ㅇ하는 것

 

–(M1 – M2) -----error----- (μ1 – μ2)

 

0가설이 트루일 때, 표준 오차는 샘플의 평균차이와 0의 표준 거리를 측정한다.

 

따라서, 표준 오차는 샘플의 평균 차이 사이즈를 측정하는 것이다.

 

-t=실제 M1 AND M2사이의 차이 /M1 AND M2 사이의 (운에따른) 표준 차이

 

-find t fomula

–t = [(sample mean difference) – (population mean difference)]

  / estimated standard error

    = [(M1 - M2) – (μ1 - μ2)]/ s(M1-M2)

    = [(M1 - M2) – (μ1 - μ2)]/ √(s2p /n1) + (s2p /n2)

 

-> 모집단 평균 사이의 차이에 대한 가설을 검증하기 위헤 샘플의 평균 사이의 차이를 사용한다.

 

-두개의 자유도 값

df1 + df2

    = (n1 -1) + (n2 -1)

    = n1 + n2 - 2

 

 

 

 

step1 : 가설을 제시하기

 

–H0: μ1 – μ2 = 0 (no difference; imagery has no effect)

–H1: μ1 – μ2 ≠ 0 (imagery produces a difference)

Step 2 : 기각역 설정하기

–df = df1 + df2 = 18

df=18 with α =.05, t=±2.101

 

step3 : 시험 통계 계산하기

 1) 합동 분산 찾기 (find pooled variance)

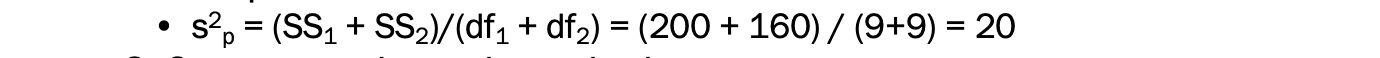
2) 추정된 표준 오차 계산하기

 

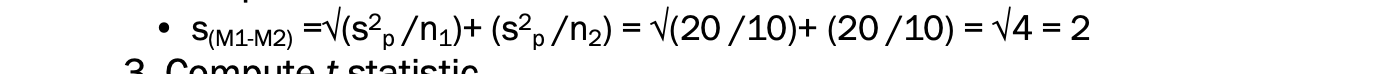
3) t 통계 계산하기

 

 

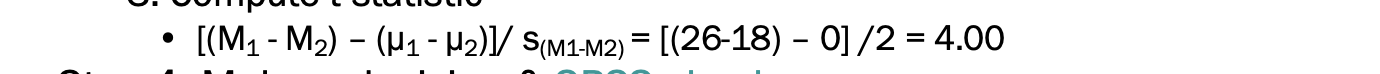
step4 : 결정을 내리기 & spss 체크하기

 

 

-유의해야 하는 것

t 통계의 크기는 두개의 샘플사이의 평균 차이에 의해 결정될 뿐만 아니라, 샘플의 변동성에 의해서도 결정된다.

 

두 샘플 평균 사이의 평균 차이가 클수록 t값은 더욱 커진다. (샘플들 사이의 큰 차이는 두 모집단들 사이의 차이를 명확하게 나타내는 지표이다.

 

샘플의 변동성은 티 통계의 표준 오차에서 중요한 요인이다. (만약에 변동성이 크다면 , 티 값은 작아질 것이다,.)

 

t=샘플의 평균 차이 / 변동성

 

- Hypothesis Tests and Effect Size with the Independent-Measures t Statistic

cohen's d= 평균 차이 / 표준편차 

독립 측정 조사 연구

d = (M1-M2) / 시그마 s^2 

 

 

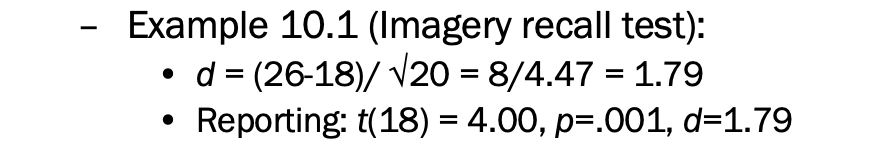
r^2 : 얼마나 소코어에서 변동성이 잘설명될 수 있는지 말하는 것 ( 결정계수)

 

 

-독립 t 측정에 대한 전제조건

1.각각의 샘플에 대한 관측은 독립적이어야 한다.

2. 샘플은 모집단으로부터 추출되었고 그 두개의 모집단은 정규분포 형태를 띄어야한다.

3.두개의 모집단은 동일한 분산을 가져야한다.

-분산의 동질성 : 비교되는 두개의 모집단은 동일한 분산을 가져야한다.

-합동 분산: 샘플의 분산들을 함께 평균화함으로써 얻어진 것이다.

두개의 값이 모집단의 분산이 동일하다고 한다면 두 값의 평균화 한다는 것은 논리적으로 알맞다.

-두개의 샘플 분산이 다른 모집단의 분산을 나타낸다면 , 그떄의 평균은 의미가 없는 것이다.

 

- 분산의 전제조건이 동질성의 전제조건을 만족하는지 아닌지는 어떻게 알 수 있을까?

두개의 샘플 분산을 바라봄으로써

두개의 모집단 분산이 동일할 때, 두 샘플의 분산들은 매우 비슷해야한다.