2023. 11. 21. 12:33ㆍ학교 수업/광고홍보조사방법론
t-test
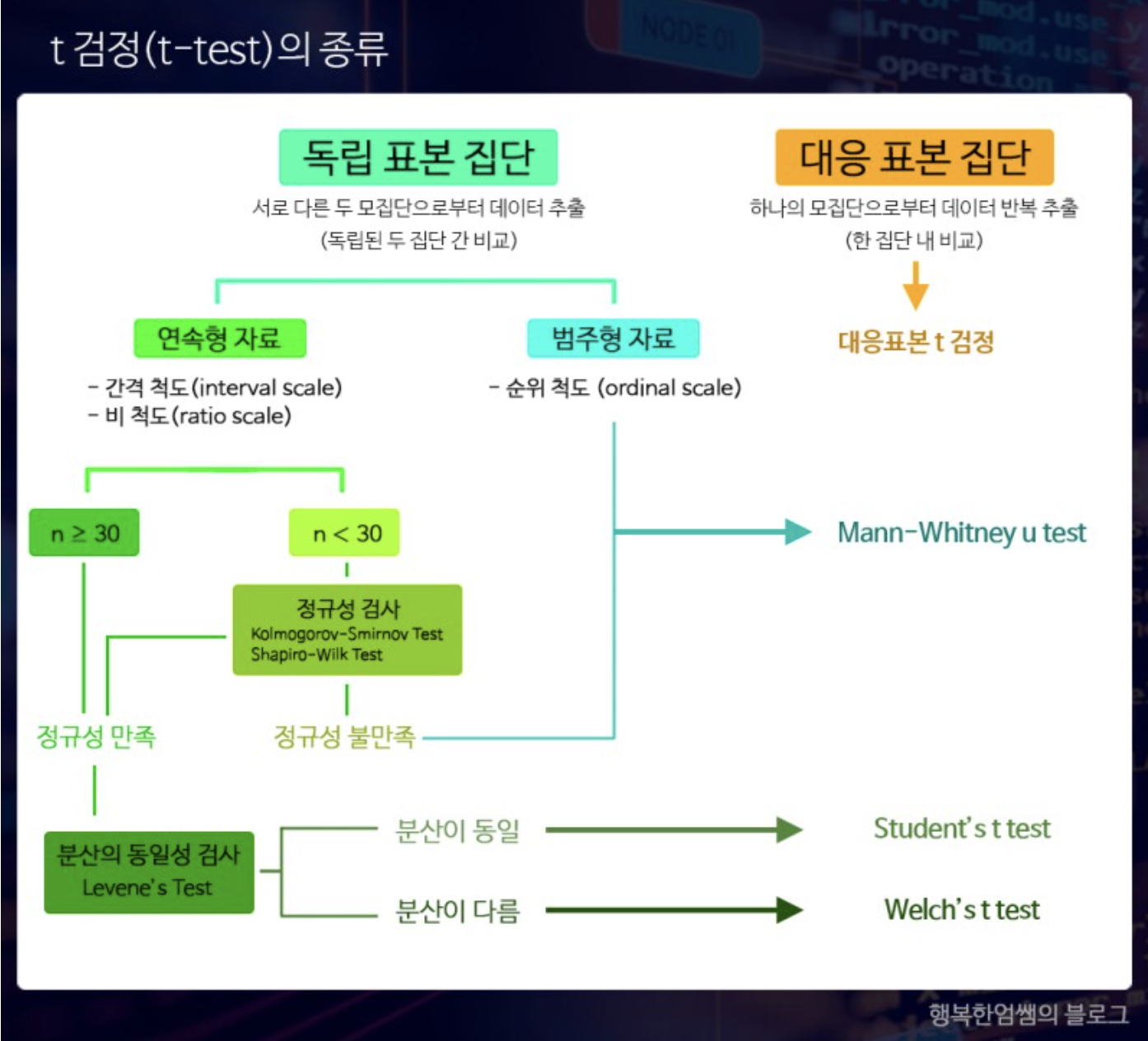
독립된 두 집단 (또는 대응표본t검정의 경우에는 한 집단)의 평균 차이가 있는지를 검사하는 방법
- 30개 이하의 비교적 적은 수의 표본에 대해 활용한다.
표본의 수가 31 이상이면 정규분포와 비슷해지기 때문에 t분포 대신 정규분포를 사용해도 괜찮다. 물론 정규분포와 일치하지는 않다. 대부분의 t분포표가 표본이 30인 경우까지만 표시하고 있기 때문에 표준정규분포표를 이용하기도 한다.)
-일반적으로 두 집단의 평균을 비교하는 분석방법은 z-test/t-test로 구분
z-test는 모집단의 분산을 알고 있는 경우에 사용되며 t-test는 모집단의 분산을 모르는 경우 사용
그러나 현실적으로 모집단의 분산을 알고 있는 경우는 거의 없기 때문에 대부분 t-test를 사용
- 모집단의 표준편차를 알 수 없을 때 사용한다. 따라서 모집단의 표준편차 σ 대신 표본의 표준편차 s 를 사용한다.
전제사항)
t-test는 비교되는 변수가 연속이어야 한다는 것 외에 두 모집단이 모두 정규 분포를 따르고 분산이 같다는 가정
t-검정 전제 사항 : 두 집단의 독립성, 정규성, 등분산성
------------------------------------------------------------------------------------------------
f분포
연속 확률 분포로 f검정과 분산분석 등에서 사용
f분포는 분산의 비교를 통해 얻어진 분포 비율
f-검정 사용 용도
-f-검정은 두 모집단의 분산의 차이가 통계적으로 유의한지 확인하는 검증 방식
(두 집단의 평균의 차이가 존재하는가가 아니라 분산의 차이가 있는가를 검정한다)
f검정 값은 항상 1보다 같거나 크다.
f값이 클수록 두 집단 간의 분산의 차이가 존재하는 것 의미
anova(분산분석, 변량분석)
둘 이상의 집단 간에 어떤 변수의 평균 점수에 차이가 있는지를 검정
집단 내의 분산, 총 평균과 각 집단의 평균 차이에 의해 생긴 집단 간 분산의 비교를 통해 만들어진 f분포를 이용하여 가설검정을 하는 방법
'학교 수업 > 광고홍보조사방법론' 카테고리의 다른 글
| ch.10 The t-Test for Two Independent Samples (0) | 2023.11.21 |
|---|---|
| 9장 t-test 티검정 (2) | 2023.11.21 |
| Ch. 6 Probability (0) | 2023.10.02 |
| z_scores 광고홍보조사방법론 9/20 (0) | 2023.09.21 |
| 광고홍보조사방법론 variability(표준편차) 9/20 (0) | 2023.09.21 |