2024. 8. 5. 16:50ㆍ대외활동/ai 유니버시티
데이터마이닝과 머신러닝
데이터마이닝의 목적 (=통찰력)
데이터를 탐색하고 분석하여 유용한 정보나 패턴을 발견하고 이를 통해 유의미한 정보를 추출하여 의사결정에 활용한다. 데이터베이스, 통계, 데이터시각화, 머신러닝 기술 등을 사용
머신러닝의 목적(=예측모델)
주어진 데이터를 학습하여 예측을 위한 모델을 구축하고 구축된 모델을 통해 자동화된 의사결정 지원
데이터 분석 방법론
CRISP-DM(CRoss Industry Standard Process for Data Mining)
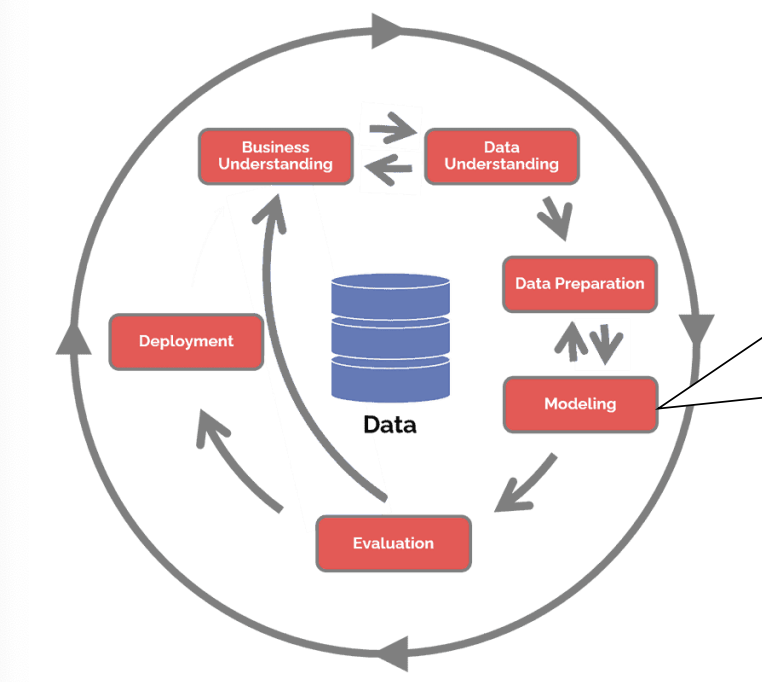
Modeling : 데이터에서 패턴을 학습하고 이를 기반으로 예측이나 분류를 수행할 수 있는 수학적 모델을 구축하는 과정
https://www.datascience-pm.com/crisp-dm-2/
What is CRISP DM? - Data Science Process Alliance
The CRoss Industry Standard Process for Data Mining (CRISP-DM) is a process model with six phases that describes the data science life cycle.
www.datascience-pm.com
1. Business Understanding
비즈니스 관점에서 프로젝트의 목적과 요구사항을 이해하기 위한 단계
수행업무
- 데이터분석을 위한 문제정의
- 데이터마이닝 목표 설정
- 초기 프로젝트 계획 수립
2. Data Understanding
분석을 위한 데이터를 수집하고 탐색적 데이터 분석(EDA)을 수행하는 단계
수행업무
- 초기 데이터 식별 및 수집
- 데이터의 속성 파악 – 속성내용, 자료형, 레코드수 등
- 데이터 품질 확인 – 결측치, 이상치 등
- 데이터 탐색 – 기술통계, 시각화, 상관관계 파악 등
3. Data Preparation
모델링을 위하여 데이터를 전처리하는 단계
수행업무
- 후보변수 선택, 파생변수 생성
- 데이터 정제 – 결측치 및 이상치 처리 등
- 데이터 변환 - 정규화, 표준화, 인코딩 등
- 데이터 통합 – 여러 소스의 데이터 결합 등
4. Modeling
모델링 기법과 알고리즘을 선택하여 모델을 구축하고 모델을 기술적으로 평가하는 단계
- 모델링 기법 선택
- 테스트 설계
- 모델 훈련
- 모델의 기술적 평가 및 파라미터 최적화
5. Evaluation
모델링 결과가 비즈니스 목적과 요구사항을 만족하는지 평가하고 다음 수행할 작업을 살펴보는 단계
수행업무
- 모델의 적용 적합성 평가
- 모델링 과정 재검토
- 다음 단계 결정 – 반복/배포/새프로젝트
6. Deployment
완성된 모델을 실 업무에 적용하기 위한 계획을 세우는 단계
수행업무
- 모델 배포계획 수립
- 모니터링 및 유지보수 계획 수립
- 프로젝트 최종보고서 작성 및 프로젝트 리뷰
머신러닝
컴퓨터가 명시적으로 프로그래밍되지 않고 데이터를 통해 학습하고 개선할 수 있는 능력을 갖추게 하는 인공지능(AI)의 한 분야
지도학습 : 레이블이 있는 훈련 데이터를 사용하여 모델을 학습시키는 방법
비지도학습 : 레이블이 없는 데이터에서 숨겨진 구조를 찾아내는 방법
강화학습 : 에이전트가 환경과 상호작용하여 보상을 최대로 하도록 학습하는 방법
준지도학습 : 레이블이 있는 데이터와 없는 데이터를 함께 사용하는 방법
실습01
https://www.kaggle.com/datasets/ashydv/advertising-dataset
Advertising Dataset
www.kaggle.com
[광고 플랫폼에 따른 판매량 예측]
문제 정의
광고 플랫폼 별 광고비에 따른 판매량 분석
- TV 광고비에 따른 판매량
- Radio 광고비에 따른 판매량
- Newspaper 광고비에 따른 판매량
*(응용)요즘으로 치면?
- SNS 유형에 따른 판매량 예측(인스타, 유튜브, 페이스북, 블로그 등)
- 인스타그램 팔로워 수에 따른 판매량 예측
import pandas as pd
import numpy as np
import matplotlib.pyplot as plt
import seaborn as sns
plt.style.use('ggplot')
df = pd.read_csv('https://raw.githubusercontent.com/JayoungKim-ai/ML_dataset/main/advertising.csv')
# 그래프 크기
plt.figure(figsize=(15,4))
# 첫번째 서브플롯
plt.subplot(1,3,1)
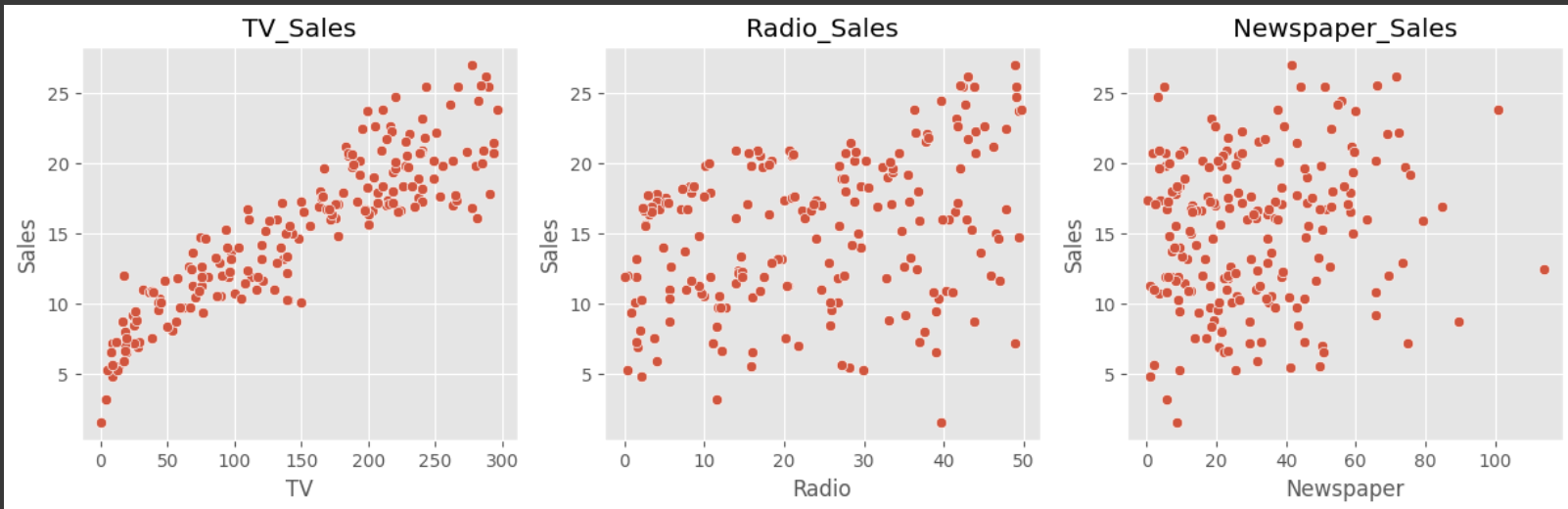
sns.scatterplot(x='TV', y='Sales', data=df)
plt.title('TV_Sales')
# 두번째 서브플롯
plt.subplot(1,3,2)
sns.scatterplot(x='Radio', y='Sales', data=df)
plt.title('Radio_Sales')
# 세번째 서브플롯
plt.subplot(1,3,3)
sns.scatterplot(x='Newspaper', y='Sales', data=df)
plt.title('Newspaper_Sales')
# 그래프 보이기
plt.show()
sns.heatmap(df.corr(), cmap='Blues', annot=True)
plt.show()
X = df['TV']
y = df['Sales']
# 훈련세트, 테스트세트 분할
from sklearn.model_selection import train_test_split
X_train, X_test, y_train, y_test = train_test_split(X, y, test_size=0.2, random_state=42)
print(X_train.shape, X_test.shape, y_train.shape, y_test.shape)
# 독립변수의 차원 변환(독립변수는 2차원이어야 함)
X_train = X_train.values.reshape(-1,1)
X_test = X_test.values.reshape(-1,1)
print(X_train.shape, X_test.shape, y_train.shape, y_test.shape)
sns.scatterplot(x=X_train.reshape(-1), y=y_train, label="train")
sns.scatterplot(x=X_test.reshape(-1), y=y_test, label="test")
plt.legend()
plt.title("train_test split")
plt.show()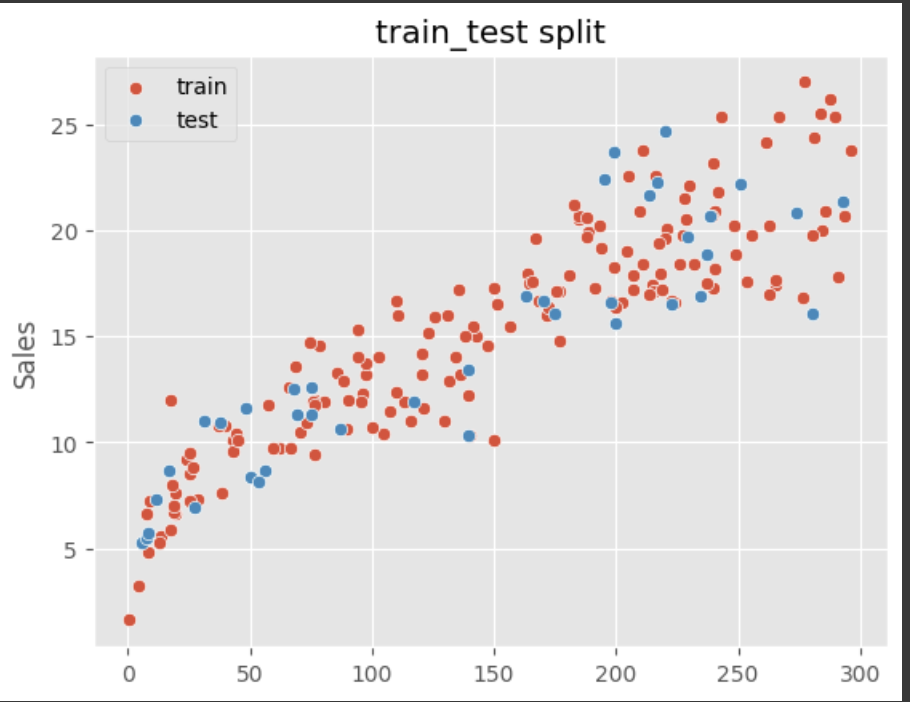
# LinearRegression 알고리즘으로 훈련하기 위해 라이브러리 불러오기
from sklearn.linear_model import LinearRegression
# 모델 생성하기
model = LinearRegression()
# 훈련데이터로 모델 훈련하기
model.fit(X_train, y_train)
# 평가 방법 선택 : MSE, R2
from sklearn.metrics import mean_squared_error, r2_score
# 테스트 데이터의 예측값
y_pred = model.predict(X_test)
# 예측값과 실제값의 차이(Loss/Error) 이용한 모델 평가
print('MSE: ', mean_squared_error(y_test, y_pred))
print('R2: ', r2_score(y_test, y_pred))
##MSE: 6.101072906773963
##R2: 0.802561303423698
print(f'기울기:{model.coef_}')
print(f'절편:{model.intercept_}')
print(f'회귀식:{model.coef_[0]} * x + {model.intercept_}')
#기울기:[0.05548294]
#절편:7.007108428241848
#회귀식:0.0554829439314632 * x + 7.007108428241848
plt.figure(figsize=(10,4))
# 테스트데이터 실제값과 예측값 확인
plt.subplot(1,2,1)
sns.scatterplot(x=X_test.reshape(-1), y=y_test, color='gray')# 테스트데이터 실제값
sns.scatterplot(x=X_test.reshape(-1), y=y_pred, color='red') # 테스트데이터 예측값
plt.ylim(0,30)
plt.title('TV_Sales Test')
# 전체 데이터, 회귀선 확인
plt.subplot(1,2,2)
sns.scatterplot(x='TV', y='Sales', data=df, color='gray') # 전체 데이터
x_line = [X.min(), X.max()]
y_line = [model.coef_*X.min()+model.intercept_, model.coef_*X.max()+model.intercept_]
plt.plot(x_line, y_line, color='red') #회귀선
plt.ylim(0,30)
plt.title('TV_Sales regression line')
plt.show()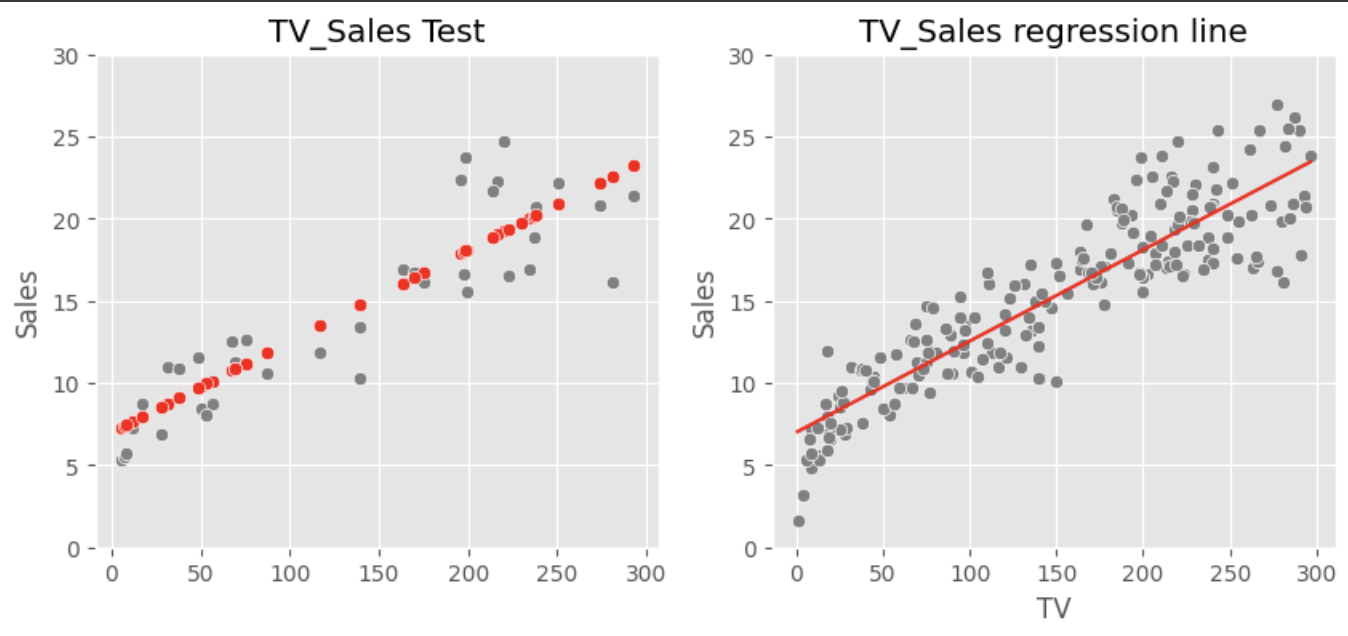
# TV 광고비 입력받기
x_tv = float(input('TV 광고비 --> '))
x_tv = np.array(x_tv).reshape(-1,1)
# 모델이 학습한 공식에 대입
print(f'{model.coef_[0] * x_tv[0,0] + model.intercept_}')
# 예측 함수 사용
print(model.predict(x_tv)[0])
다중회귀
X = df[['TV', 'Radio']]
y = df['Sales']
#데이터 분포의 차이
#큰 범위를 가진 특성이 작은 범위의 특성보다 모델에 더 큰 영향을 미칠 수 있다.
#예: 연봉(수백만 단위)과 나이(수십 단위)를 비교할 때, 스케일링 없이는 연봉이 과도하게 중요시될 수 있다.
#선형 모델이나 신경망은 가중치를 통해 각 특징의 중요성을 평가한다. 값의 범위가 큰 변수는 더 큰 가중치를 가질 가능성이 높고, 이는 모델이 이 변수에 과도하게 의존하게 만들 수 있다. 반면, 값의 범위가 작은 변수는 상대적으로 무시될 수 있다. 이로 인해 모델이 데이터를 제대로 학습하지 못하고 편향된 예측을 할 수 있다.
sns.histplot(df['TV'], bins=20, kde=True, label='TV')
sns.histplot(df['Radio'], bins=20, kde=True, label='Radio')
plt.legend()
plt.show()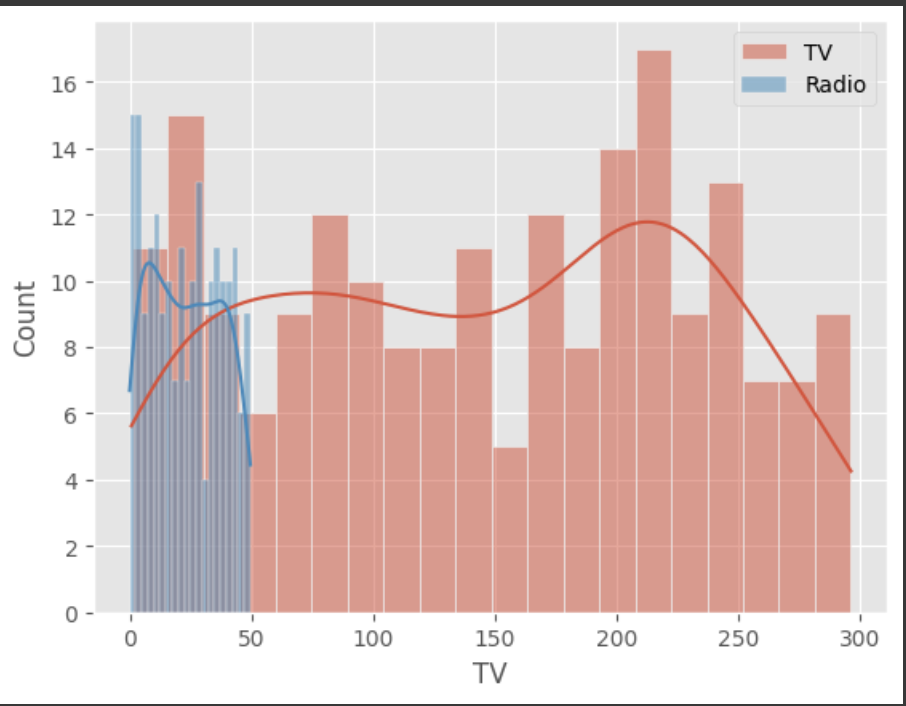
- 표준화(Standardization)
- 값의 범위를 평균이 1이고 표준편차가 1이 되도록 변환
- 정규 분포를 가정하는 모델: 선형 회귀, 로지스틱 회귀, SVM 등과 같은 모델은 변수들이 정규 분포를 따를 때 더 잘 작동할 수 있다.
# 표준화
from sklearn.preprocessing import StandardScaler
scaler = StandardScaler()
X_scaled = scaler.fit_transform(df[['TV','Radio']])
# 스케일링 한 데이터 확인
print(X_scaled[:,0].mean(), X_scaled[:,1].mean())
print(X_scaled[:,0].std(), X_scaled[:,1].std())
#1.2212453270876723e-16 -4.529709940470639e-16
#1.0 1.0
# 스케일링 후 데이터 분포
sns.histplot(X_scaled[:,0], bins=20, kde=True, label='TV')
sns.histplot(X_scaled[:,1], bins=20, kde=True, label='Radio')
plt.legend()
plt.show()
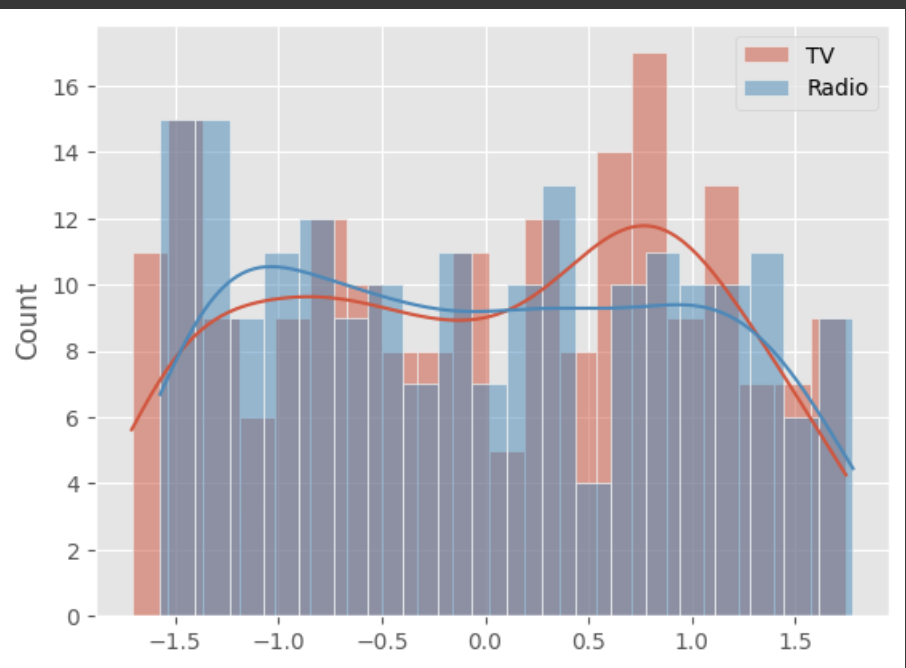
from sklearn.model_selection import train_test_split
X_train, X_test, y_train, y_test = train_test_split(X_scaled, y, test_size=0.2, random_state=42)
print(X_train.shape, X_test.shape, y_train.shape, y_test.shape)
# LinearRegression 알고리즘으로 훈련하기 위해 라이브러리 불러오기
from sklearn.linear_model import LinearRegression
# 모델 생성하기
model = LinearRegression()
# 훈련데이터로 모델 훈련하기
model.fit(X_train, y_train)
# 평가 방법 선택 : MSE, R2
from sklearn.metrics import mean_squared_error, r2_score
# 테스트 데이터의 예측값
y_pred = model.predict(X_test)
# 예측값과 실제값의 차이(Loss/Error) 이용한 모델 평가
print('MSE: ', mean_squared_error(y_test, y_pred))
print('R2: ', r2_score(y_test, y_pred))
#MSE: 2.8466161221315427
#R2: 0.907879780262465
#과적합 확인하기
# 훈련 데이터의 예측값
y_pred = model.predict(X_train)
# 예측값과 실제값의 차이(Loss/Error) 이용한 모델 평가
print('MSE: ', mean_squared_error(y_train, y_pred))
print('R2: ', r2_score(y_train, y_pred))
#기울기:[4.66797404 1.52920902]
#절편:15.20846608247682
#회귀식:4.6679740362119535 * x_tv + 1.5292090220638832 * x_radio + 15.20846608247682
print(f'기울기:{model.coef_}')
print(f'절편:{model.intercept_}')
print(f'회귀식:{model.coef_[0]} * x_tv + {model.coef_[1]} * x_radio + {model.intercept_}')
# TV 광고비 입력받기
x_tv = float(input('TV 광고비 --> '))
# radio 광고비 입력받기
x_radio = float(input('radio 광고비 --> '))
# 입력값 스케일링
x_new = scaler.transform([[x_tv, x_radio]])
# 모델이 학습한 공식에 대입
print(f'{model.coef_[0] * x_new[0,0] + model.coef_[1] * x_new[0,1] + model.intercept_}')
# 예측 함수 사용
print(model.predict([[x_new[0,0],x_new[0,1]]])[0])

#변수를 추가한 경우
print(f'기울기:{model.coef_}')
print(f'절편:{model.intercept_}')
print(f'회귀식:{model.coef_[0]} * x_tv + {model.coef_[1]} * x_radio +{model.coef_[2]}* {model.intercept_}')
Logistic Regression
로지스틱 회귀 개념
- 종속 변수가 범주형일 때, 수행할 수 있는 회귀분석 기법의 한 종류
- 독립변수들의 선형 결합을 이용하여 개별 관측치가 속하는 집단을 확률로 예측
- 선형회귀의 출력값을 시그모이드 함수에 입력하여 0~1 사이의 확률로변환
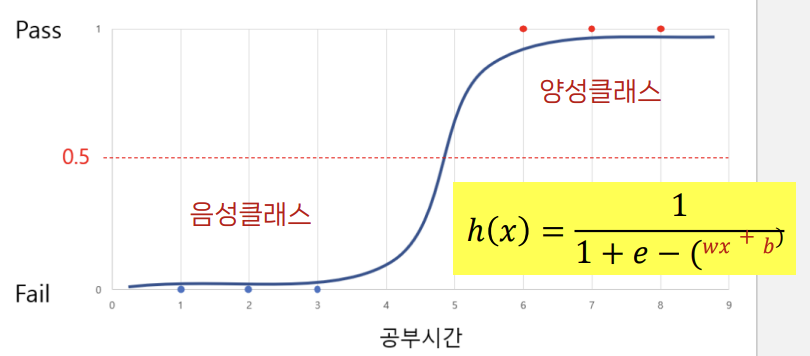
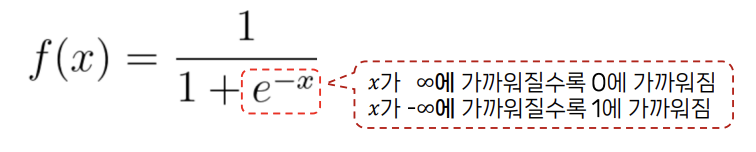
시그모이드 함수(로지스틱 함수)
결과를 0과 1 사이의 확률로 변환하는 함수
로지스틱 회귀에서는 종속 변수의 값이 0과 1 사이의 확률을 나타내야 하기 때문에, 예측 값이 이 범위 내에 있도록 제한한다.
이를 위해 시그모이드 함수라는 S-형 곡선을 사용한다. 이 함수는 모든 입력값을 0과 1 사이의 값으로 대응시킨다.
02실습 : 정기예금 가입 여부 예측
문제 정의 : 은행의 마케팅 캠페인 데이터를 사용하여 고객의 가입 여부를 예측
- 목표: 고객의 정기예금 가입 여부 예측
- 입력 데이터: 고객의 다양한 특성 정보
- 방법: 분류 모델 개발
- 비즈니스 컨텍스트: 은행의 텔레마케팅 캠페인
import pandas as pd
import numpy as np
import matplotlib.pyplot as plt
import seaborn as sns
# 그래프 스타일 설정
plt.style.use('ggplot')
# 사용자 정의 팔레트
custom_palette = {'yes': 'cyan', 'no': 'gray'}
df = pd.read_csv('https://raw.githubusercontent.com/JayoungKim-ai/ML_dataset/main/bank.csv')
# 컬럼 및 독립변수와 종속변수 확인
display(df.head())
display(df.tail())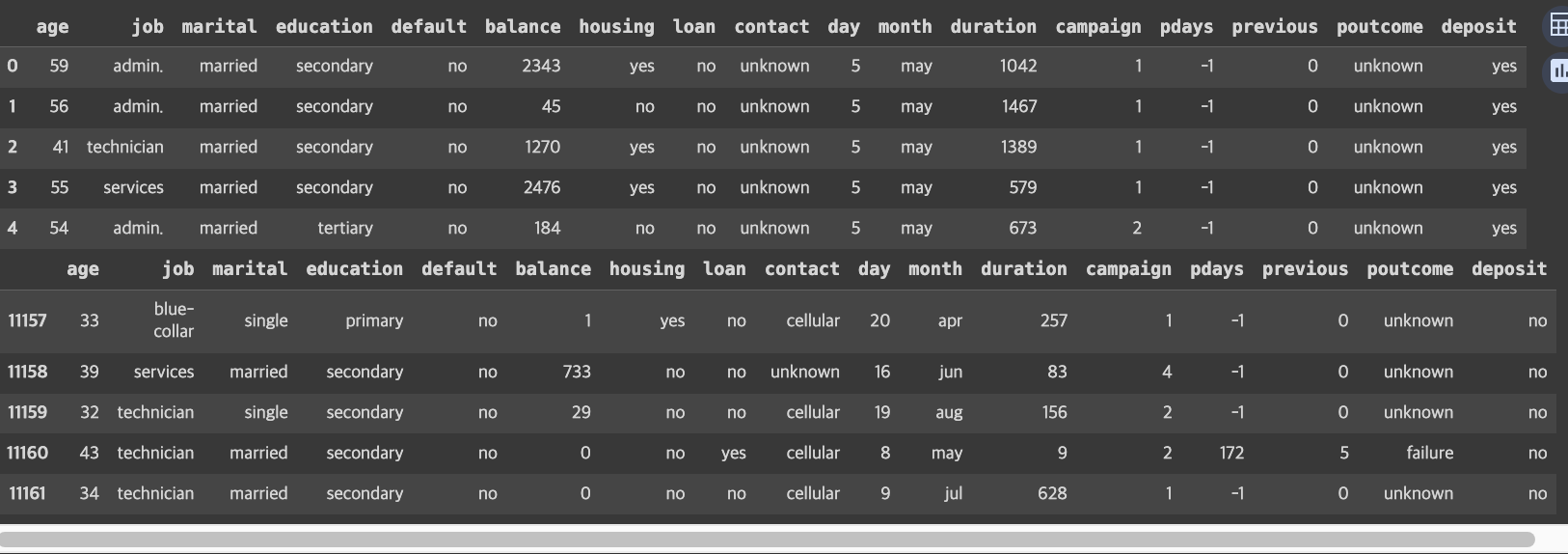
데이터 탐색
- 데이터의 분포
- 종속변수(deposit)와의 관계
plt.pie(df['deposit'].value_counts(), labels=df['deposit'].value_counts().index, autopct='%1.1f%%', colors=['gray','cyan'])
plt.title('Deposit Distribution')
plt.show()
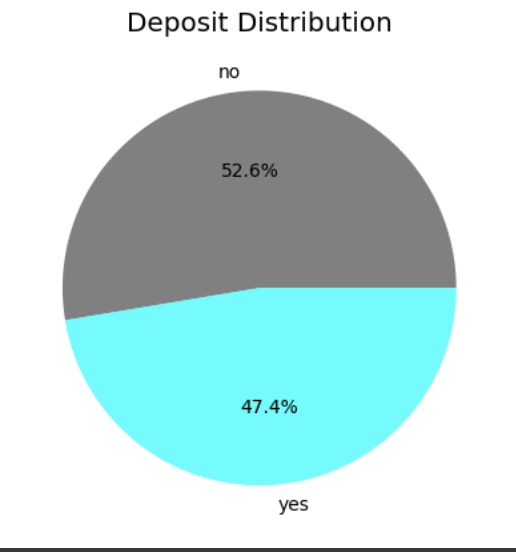
비율이 균등하게 나타났지만, 질병 같은 경우 비균등한 결과가 나타날 수 있음(질병 o=1, x=9) 이런 경우 다른 전처리를 진행해야함.
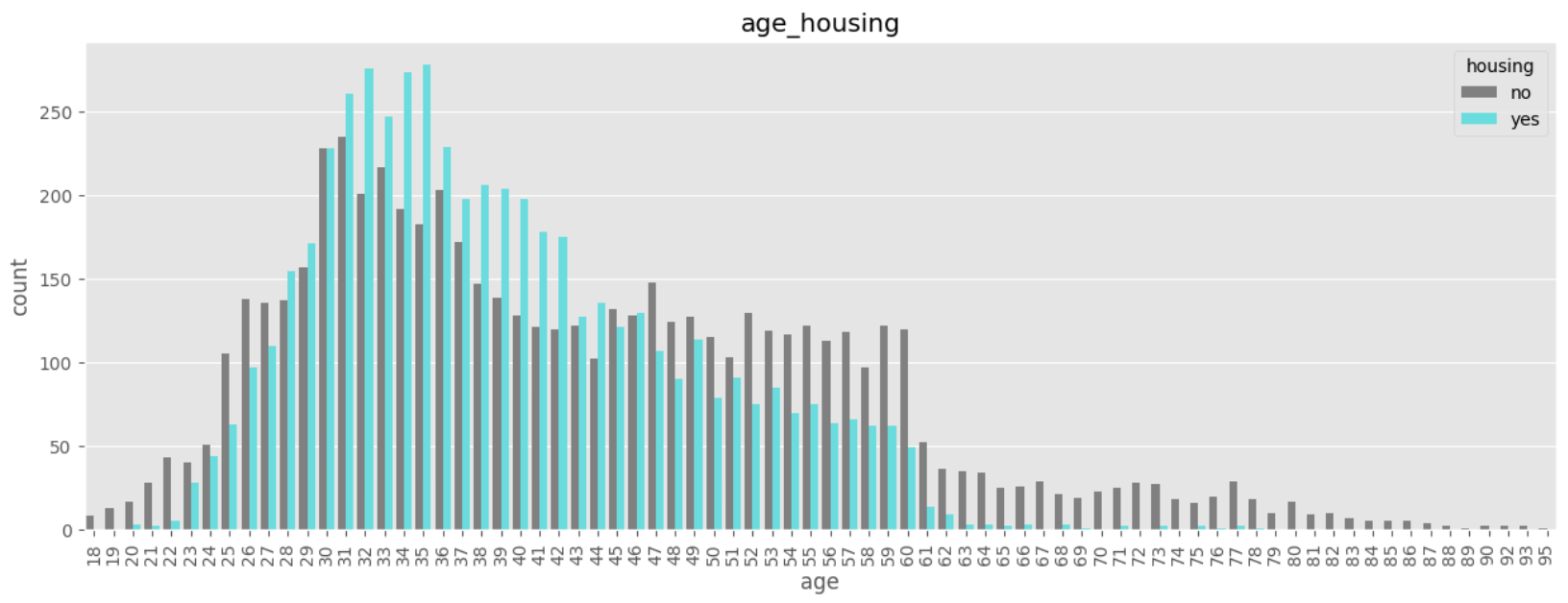
# age
# 18세~95세
# 30~59세 : 정기예금 가입율이 낮음
# why?
# 자녀 양육비용? 주택구입으로 인한 대출? 다른 재테크 수단?
plt.figure(figsize=(15,5))
sns.countplot(x='age', data=df, hue='deposit', palette=custom_palette)
plt.xticks(rotation=90)
plt.title('age_deposit')
plt.show()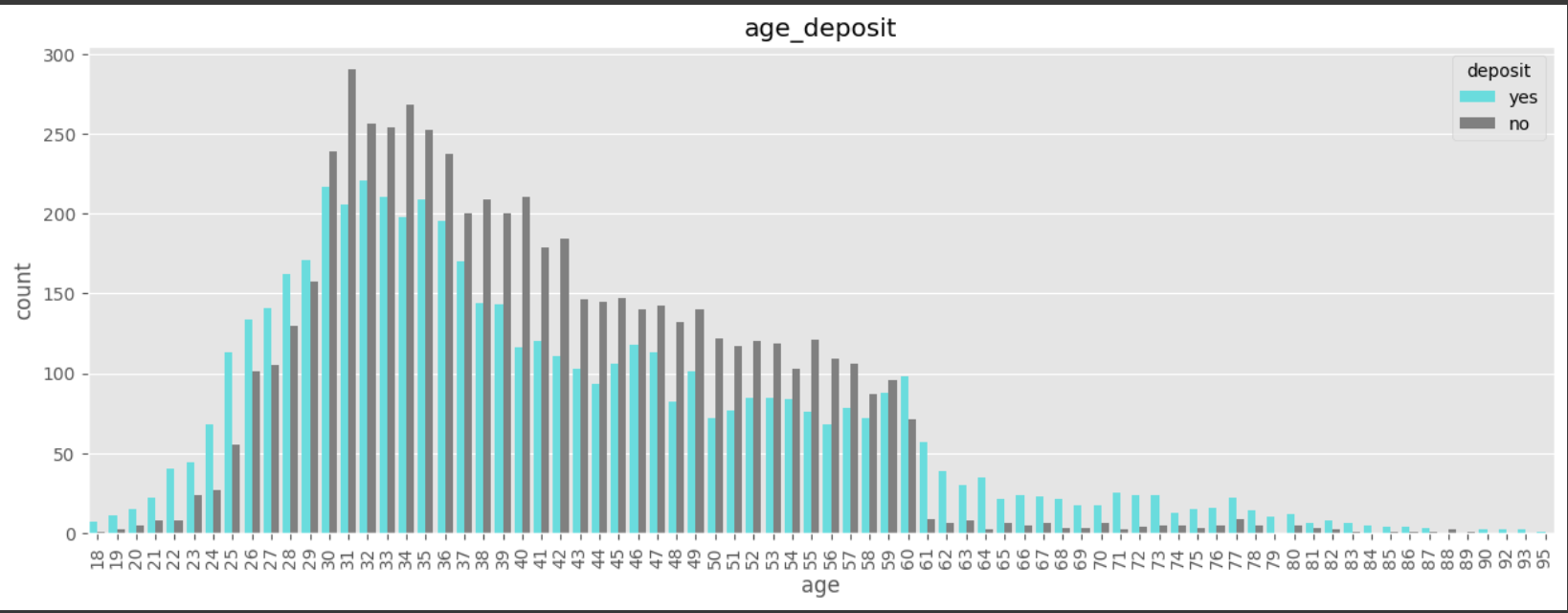
eda를 통하여 데이터 분포를 파악 -> 차이가 발생한 데이터에 대하여 인과관계를 찾는 과정 필요
# job
# 은퇴자, 실직자, 학생 정기예금 가입율이 높음
# 블루컬러 정기예금 가입율 특히 낮음
sns.countplot(x='job', data=df, hue='deposit', palette=custom_palette)
plt.xticks(rotation=90)
plt.title('job_deposit')
plt.show()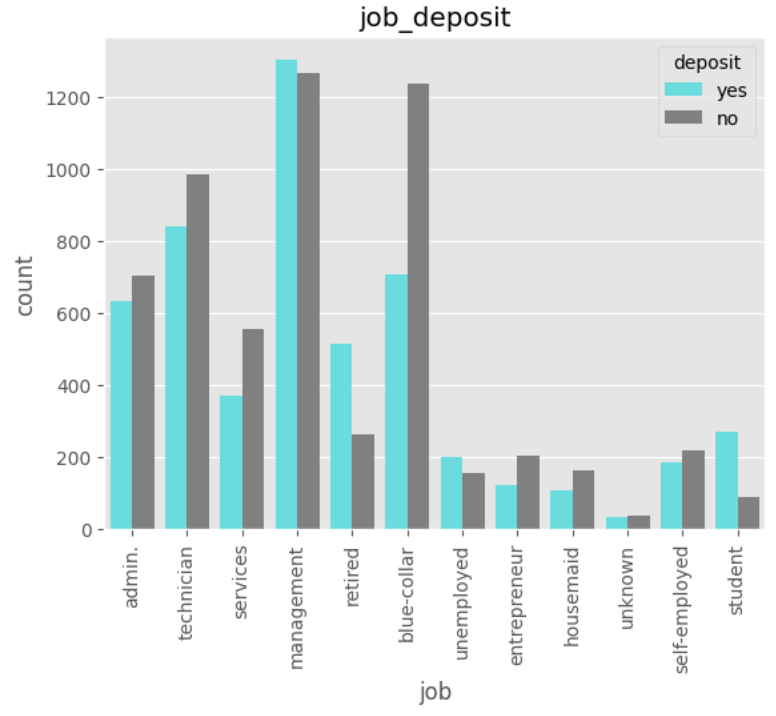
# marital
sns.countplot(x='marital', data=df, hue='deposit', palette=custom_palette)
plt.xticks(rotation=90)
plt.title('marital_deposit')
plt.show()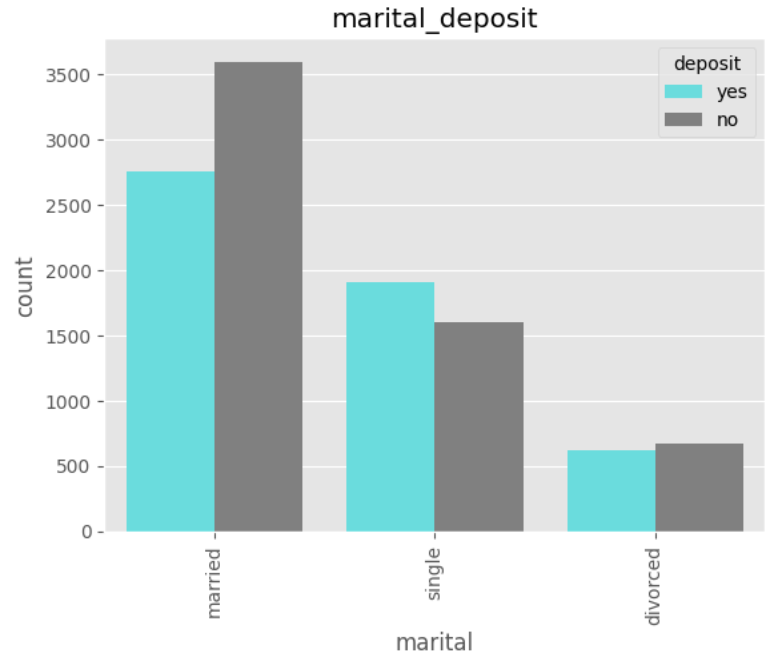
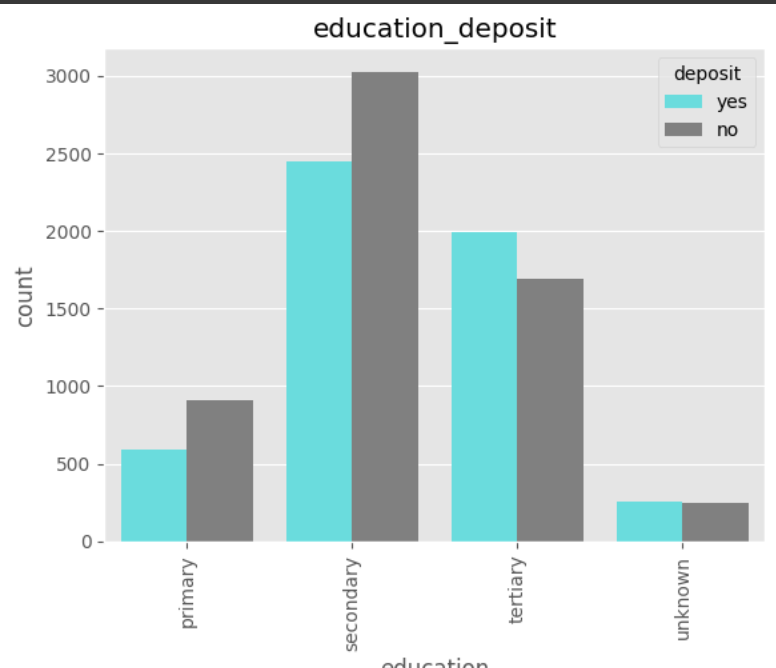
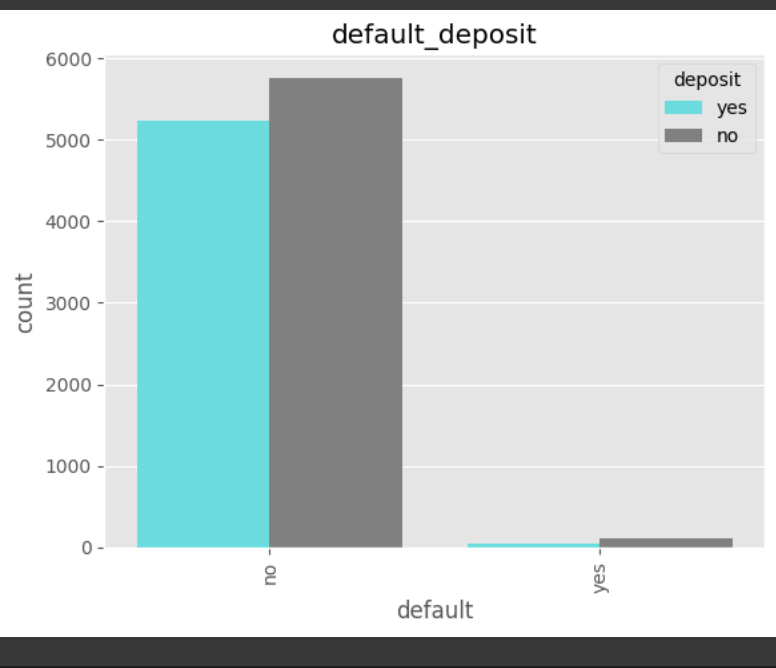
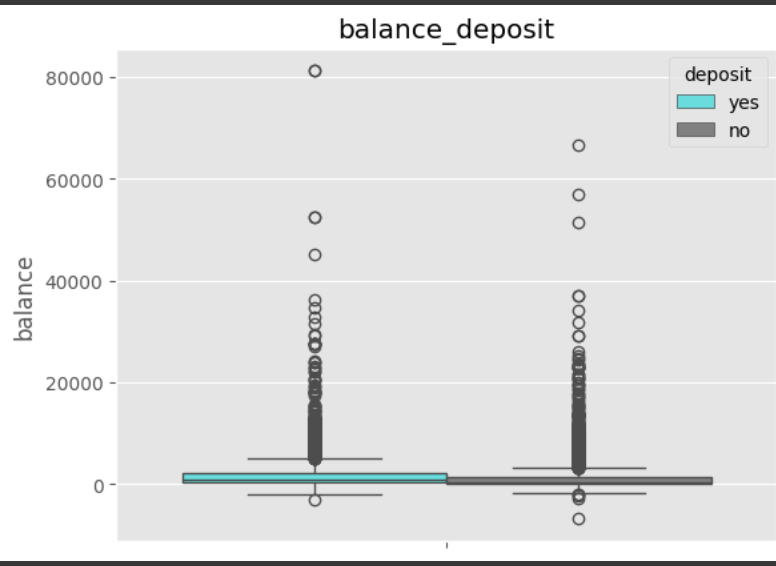
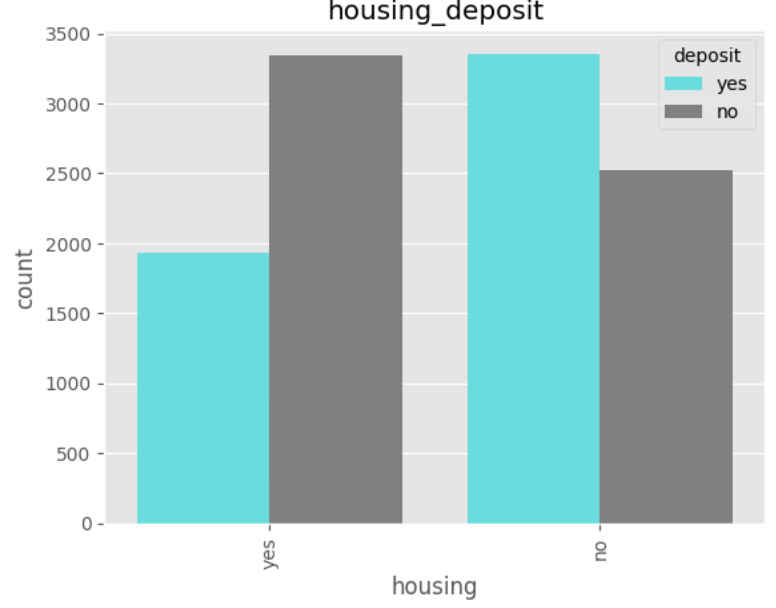
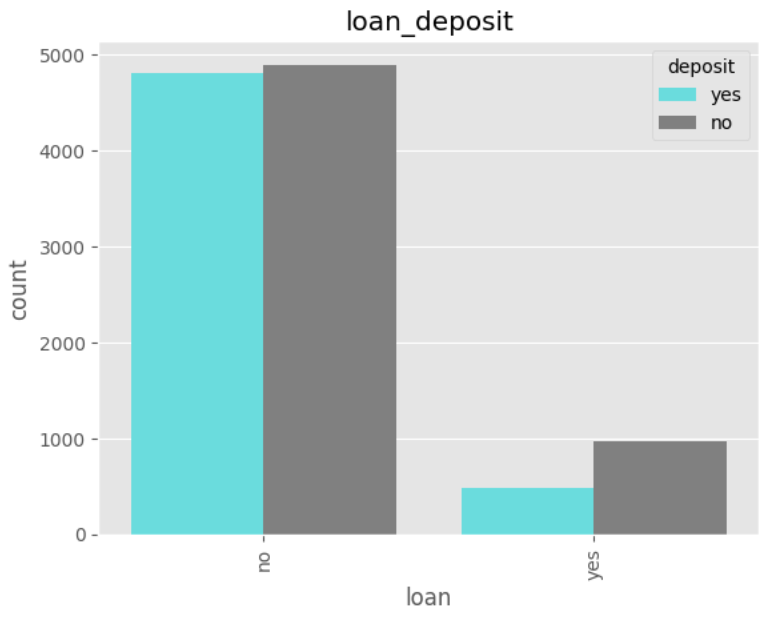
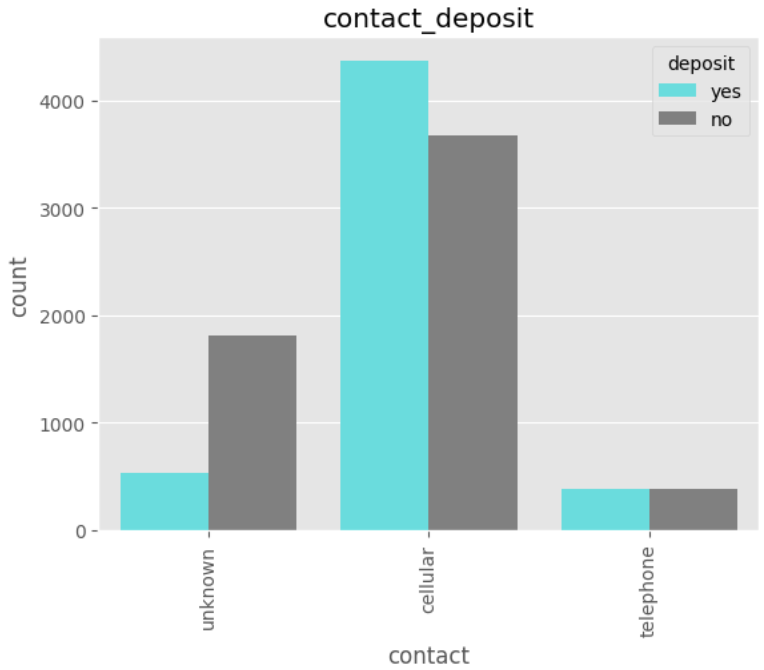
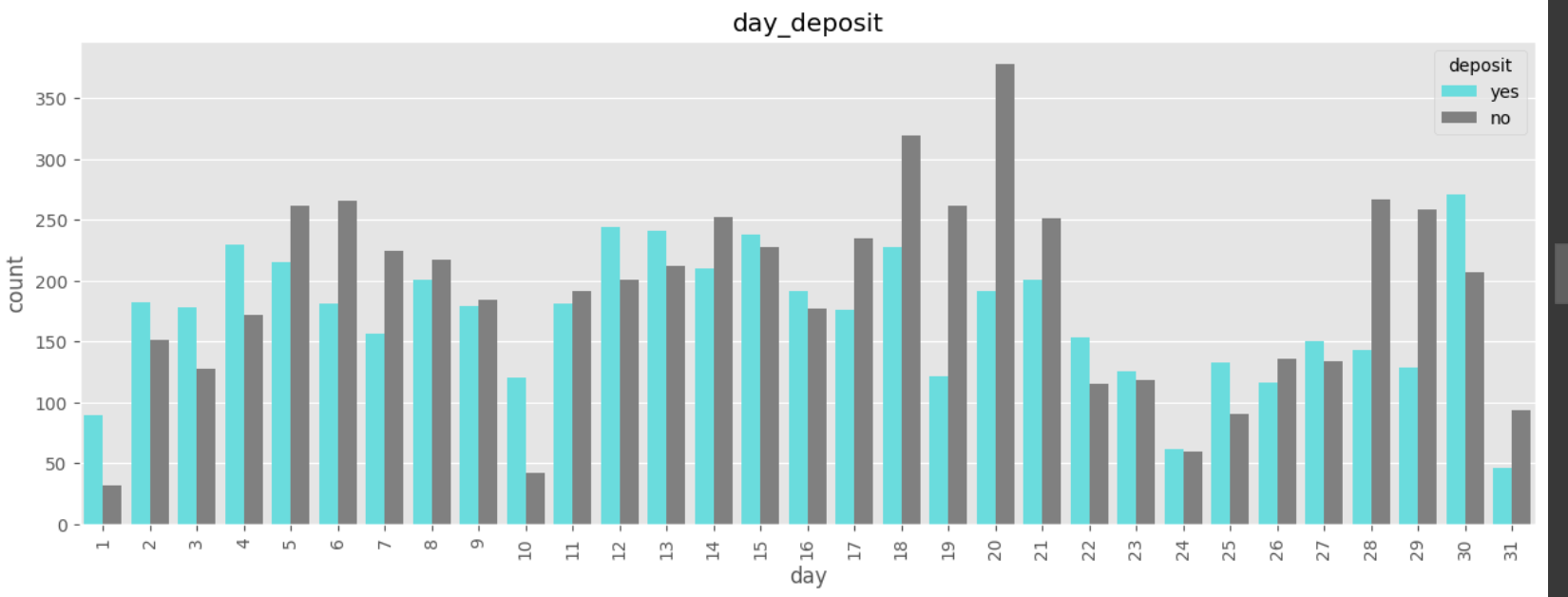
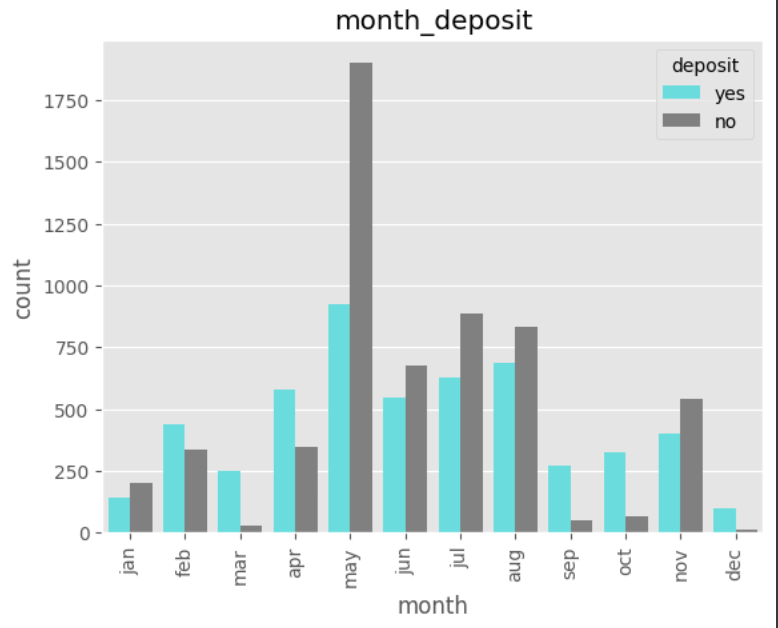
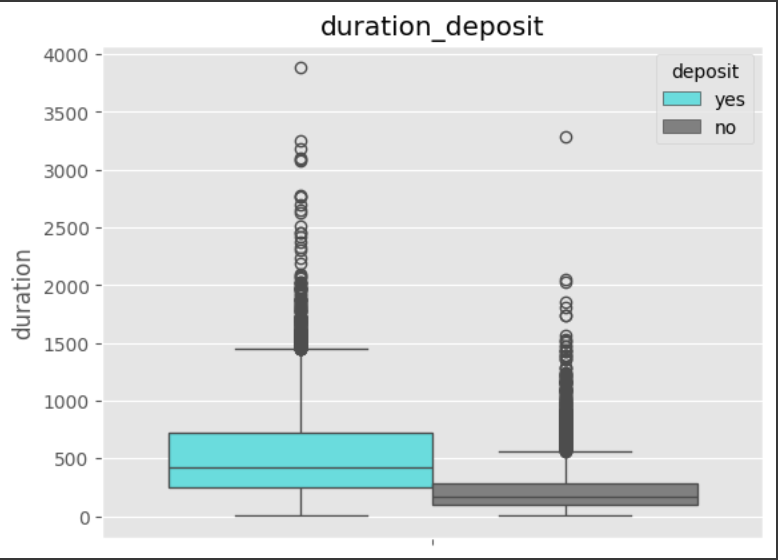
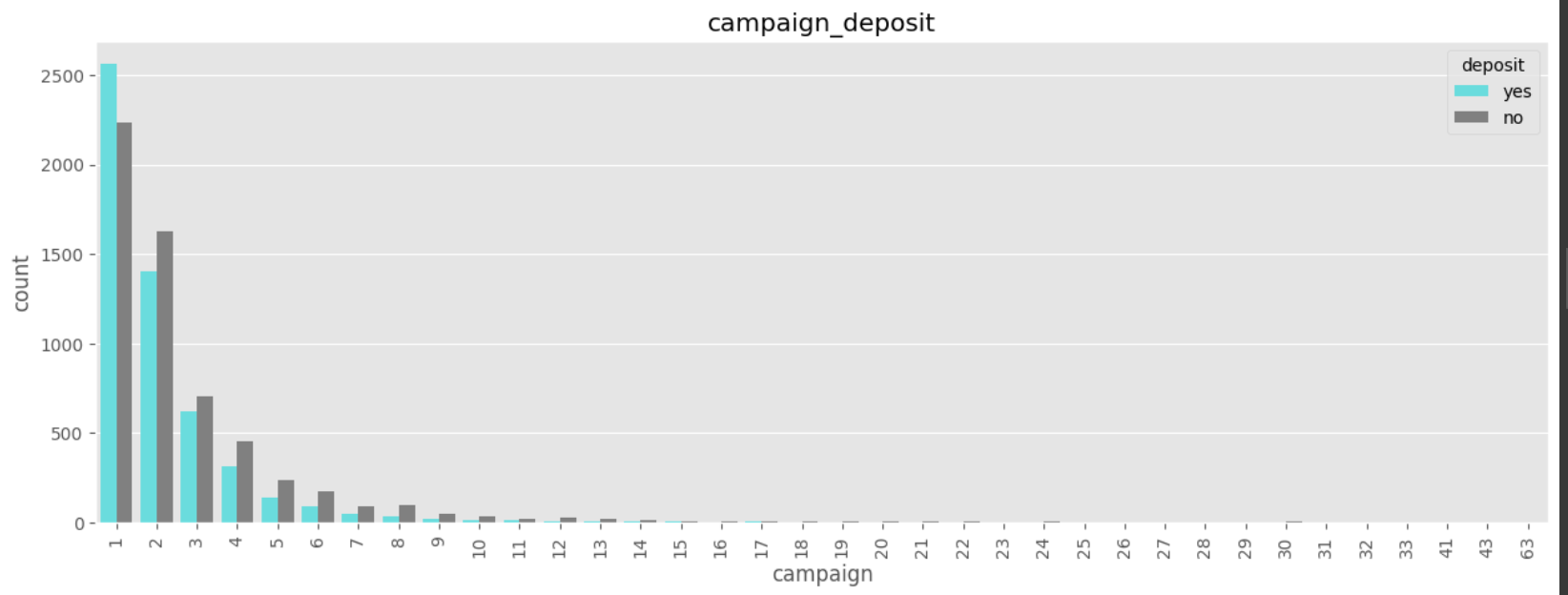
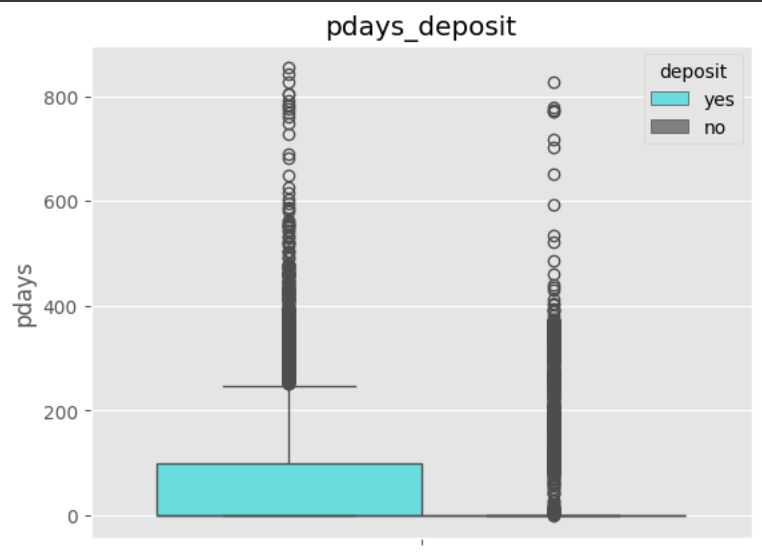
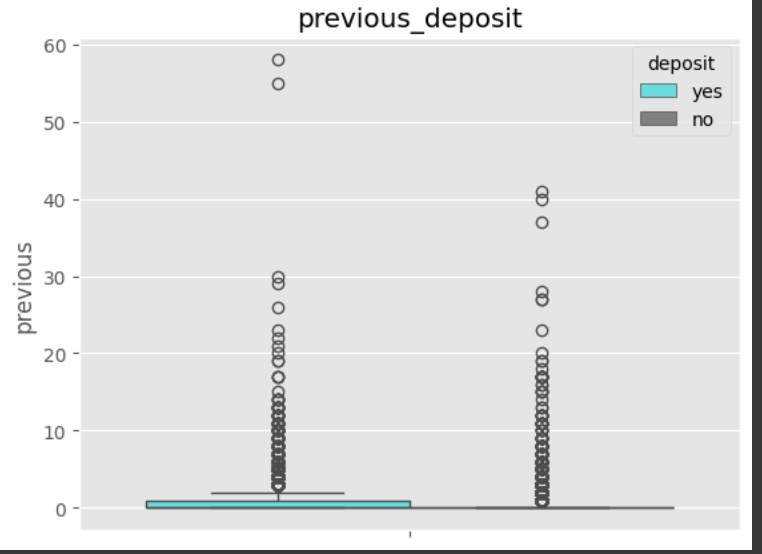
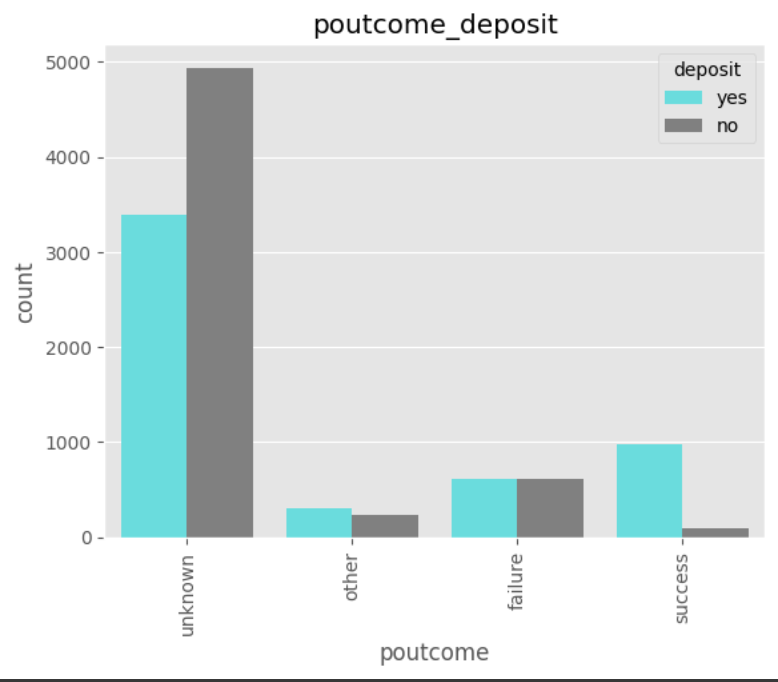
데이터 전처리
# 독립변수와 종속변수 분리
X = df.drop('deposit', axis=1)
y = df['deposit']
#종속변수의 데이터 변환
y = y.map({'yes': 1, 'no': 0})
y
# 범주형 변수의 레이블 인코딩
# 범주형 변수만 추출하기
objs = X.select_dtypes(include="object").columns.tolist()
# 수치형 변수만 추출하기
nums = df.select_dtypes(exclude="object").columns.tolist()
print(objs)
print(nums)
#['job', 'marital', 'education', 'default', 'housing', 'loan', 'contact', 'month', 'poutcome']
#['age', 'balance', 'day', 'duration', 'campaign', 'pdays', 'previous']
from sklearn.preprocessing import LabelEncoder
# LabelEncoder 객체를 저장할 딕셔너리
encoders = {}
# 원본은 그대로 두고 복사본으로 작업
X_preprocessed = X.copy()
# 각 열에 대해 레이블 인코딩 수행
for obj in objs:
le = LabelEncoder()
X_preprocessed[obj] = le.fit_transform(X[obj])
encoders[obj] = le # 각 열의 LabelEncoder 저장
# 인코딩된 결과 확인
for obj in objs:
print(f"Column: {obj}")
print(f"Classes: {encoders[obj].classes_}")
print(f"Encoded Values: {X_preprocessed[obj].unique()}")
print()
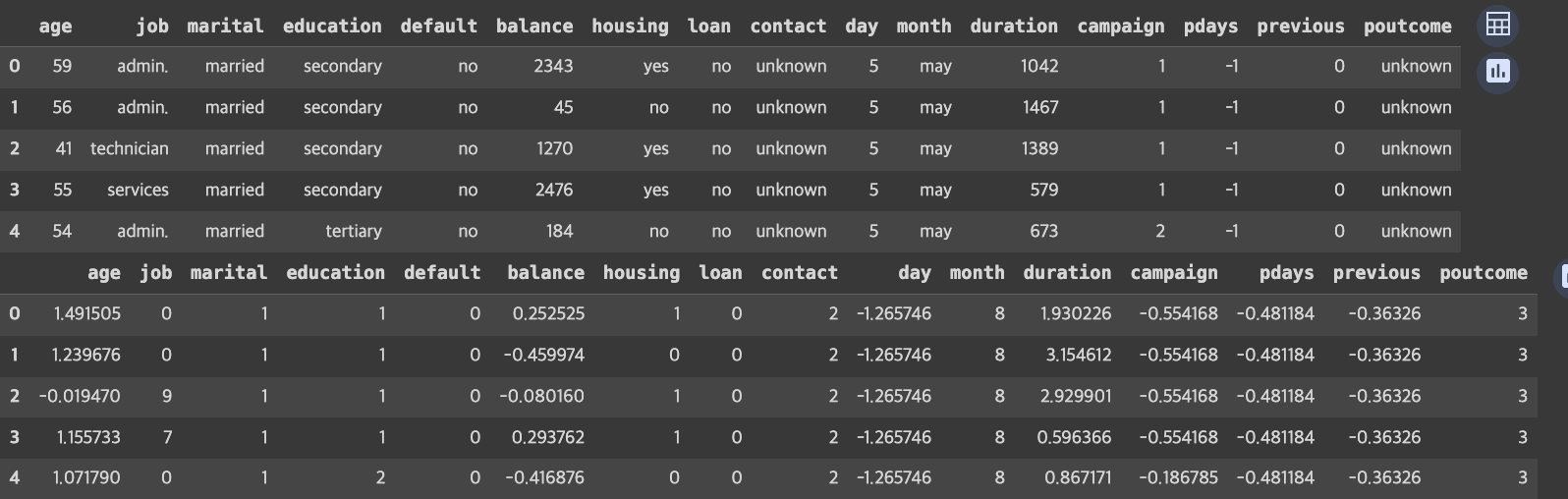
display(X.head())
display(X_preprocessed.head())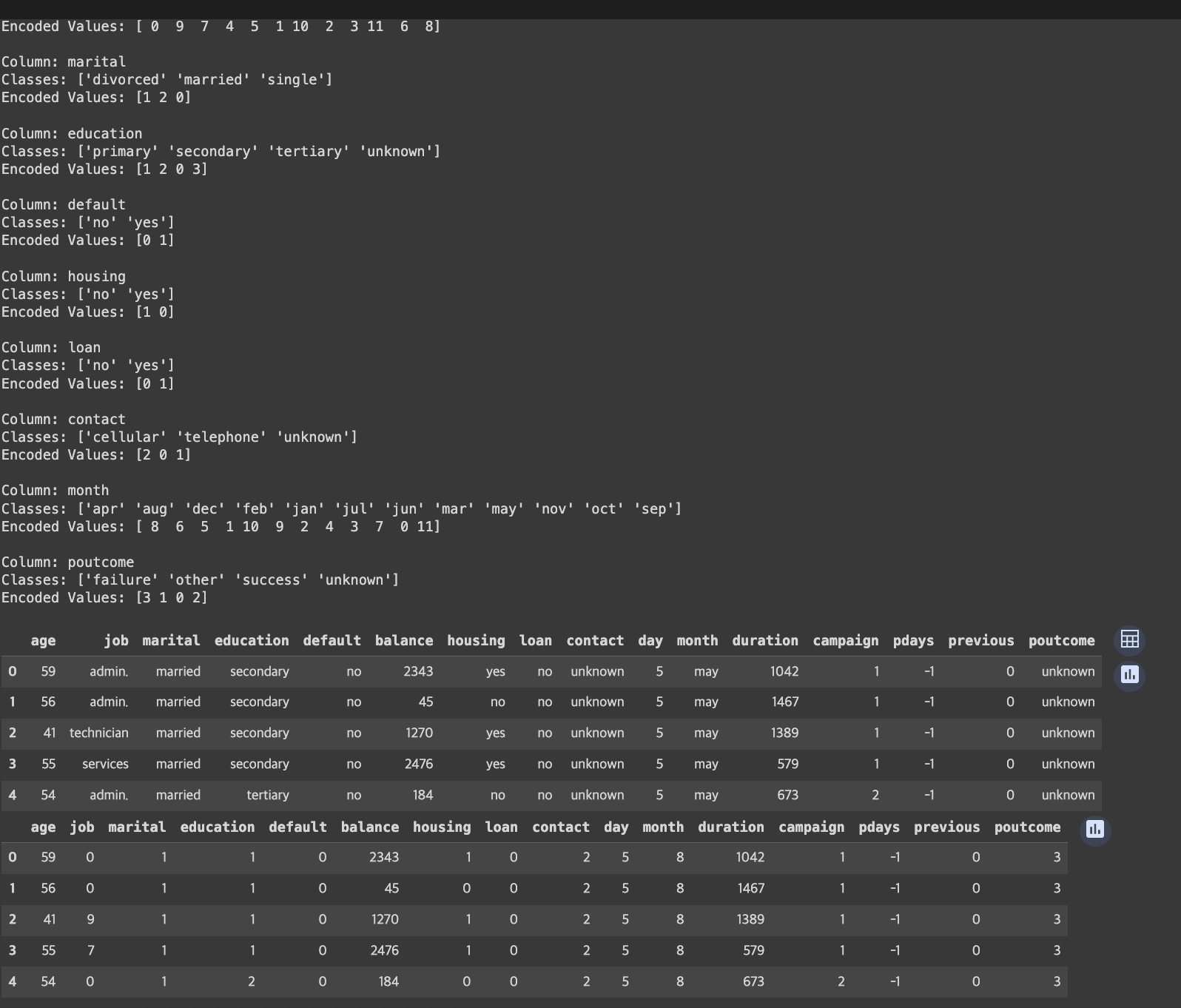
# 수치형데이터의 스케일링
from sklearn.preprocessing import StandardScaler
scaler = StandardScaler()
X_preprocessed[nums] = scaler.fit_transform(X[nums])
display(X.head())
display(X_preprocessed.head())
* 변수 중요도 평가(SelectKBest.. )
import numpy as np
import pandas as pd
from sklearn.feature_selection import SelectKBest, f_classif, chi2
# df_preprocessed: 레이블 인코딩된 데이터프레임
# objs: 범주형 변수들의 이름 리스트
# nums: 연속형 변수들의 이름 리스트
# 범주형 변수와 수치형 변후 분리
X_objs = X_preprocessed[objs]
X_nums = X_preprocessed[nums]
# 범주형 변수에 대해 chi2 사용
selector_cat = SelectKBest(score_func=chi2, k='all')
X_new_cat = selector_cat.fit_transform(X_objs, y)
selected_cat_indices = selector_cat.get_support(indices=True)
selected_cat_features = X_objs.columns[selected_cat_indices]
cat_scores = selector_cat.scores_[selected_cat_indices]
# 연속형 변수에 대해 f_classif 사용
selector_cont = SelectKBest(score_func=f_classif, k='all')
X_new_cont = selector_cont.fit_transform(X_nums, y)
selected_cont_indices = selector_cont.get_support(indices=True)
selected_cont_features = X_nums.columns[selected_cont_indices]
cont_scores = selector_cont.scores_[selected_cont_indices]
# 점수와 특성을 데이터프레임으로 결합
selected_features_df = pd.DataFrame({
'Feature': selected_cat_features.tolist() + selected_cont_features.tolist(),
'Score': np.concatenate([cat_scores, cont_scores])
})
# 점수 기준으로 정렬
selected_features_df = selected_features_df.sort_values(by='Score', ascending=False)
print("Features sorted by importance:")
print(selected_features_df)
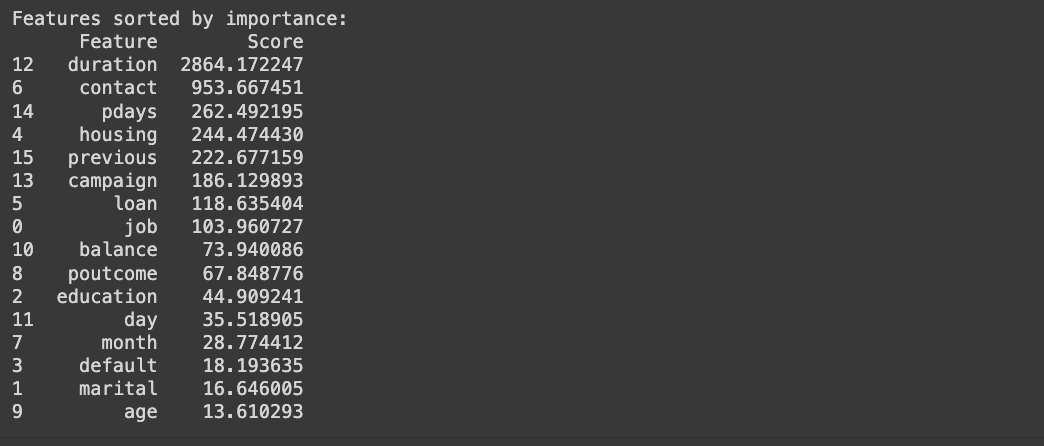
도메인 지식 등에 따라 변수 선택 여부가 달라질 수 있음
# 다중공선성 : 수치형 변수간의 상관관계 확인
sns.heatmap(abs(X_preprocessed[nums].corr()), cmap='Blues', annot=True)
plt.show()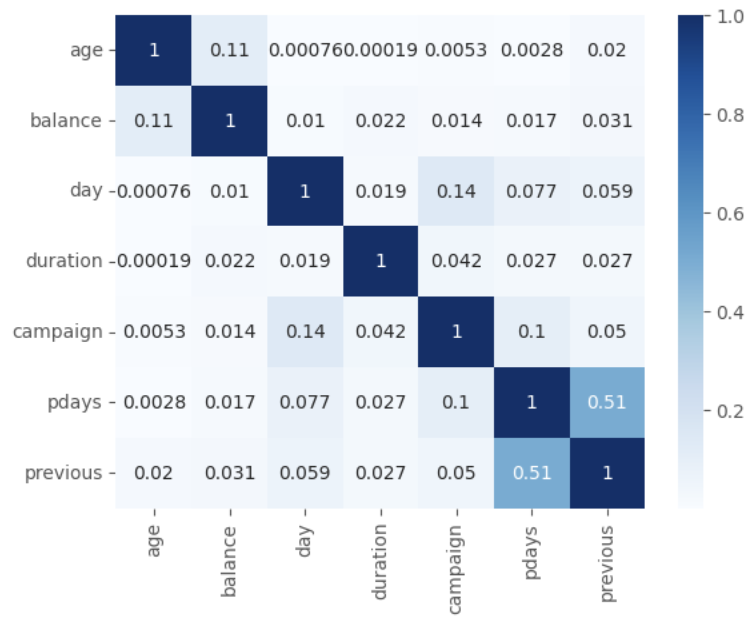
*다중공산성 문제 방지를 위하여 상관관계가 높은 변수를 제거하는 과정을 거치기도 함
# 훈련 및 테스트 데이터 분할
from sklearn.model_selection import train_test_split
X_train, X_test, y_train, y_test = train_test_split(X_preprocessed, y, test_size=0.2, random_state=42)
X_train.shape, X_test.shape, y_train.shape, y_test.shape
from sklearn.linear_model import LogisticRegression
#LogisticRegression
# 모델 생성
model_lr = LogisticRegression()
# 훈련데이터로 학습
model_lr.fit(X_train, y_train)
# 예측값
y_pred = model_lr.predict(X_test)
# 정확도
from sklearn.metrics import accuracy_score
print("accuracy_score:", accuracy_score(y_test, y_pred))
# 과적합 확인
print("test accuracy:", model_lr.score(X_test, y_test))
print("train accuracy:", model_lr.score(X_train, y_train))
정확도 : 전체 데이터 중 몇개를 맞췄는지에 대한 평가지표(= 100개 중 78개를 맞춤)
# 모델이 학습한 결과
# lr 모델의 계수(coefficients)
print("Coefficients:", model_lr.coef_)
# lr 모델의 절편(intercept)
print("Intercept:", model_lr.intercept_)
# 모델의 성능 평가
# 테스트 데이터 예측
y_pred = model_lr.predict(X_test)
# 모델의 평가 지표
from sklearn.metrics import classification_report
print("\nClassification Report:\n", classification_report(y_test, y_pred))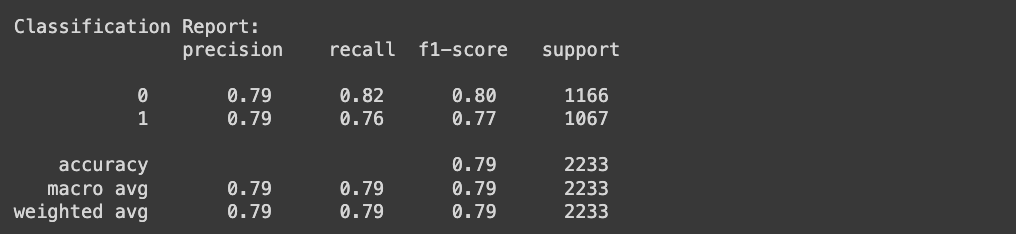
classification_report : 평가지표를 보여주는 함수
# 혼동행렬
from sklearn.metrics import confusion_matrix
cm = confusion_matrix(y_test, y_pred)
plt.figure(figsize=(4, 4))
sns.heatmap(cm, annot=True, fmt='d', cmap='Blues', xticklabels=['Predicted 0', 'Predicted 1'], yticklabels=['Actual 0', 'Actual 1'])
plt.xlabel('Predicted Label')
plt.ylabel('Actual Label')
plt.title('Confusion Matrix')
plt.show()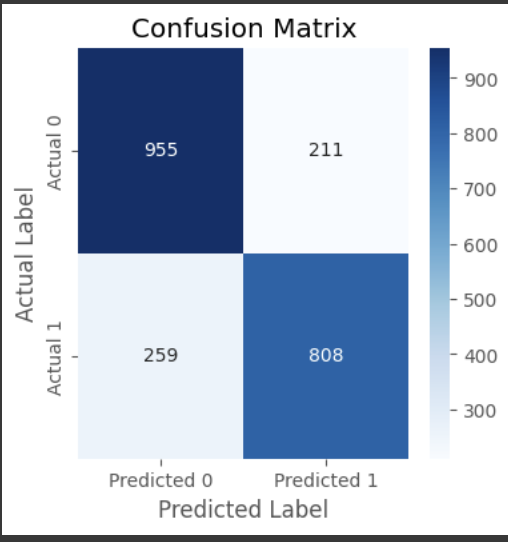
# roc_auc
import matplotlib.pyplot as plt
from sklearn.metrics import roc_curve, roc_auc_score
# 예측 확률 계산
y_pred_proba = model_lr.predict_proba(X_test)[:, 1]
# ROC 곡선 계산
fpr, tpr, thresholds = roc_curve(y_test, y_pred_proba)
roc_auc = roc_auc_score(y_test, y_pred_proba)
# ROC 곡선 그리기
plt.figure()
plt.plot(fpr, tpr, color='darkorange', lw=2, label='ROC curve (area = %0.2f)' % roc_auc)
plt.plot([0, 1], [0, 1], color='navy', lw=2, linestyle='--')
plt.xlim([0.0, 1.0])
plt.ylim([0.0, 1.05])
plt.xlabel('False Positive Rate')
plt.ylabel('True Positive Rate')
plt.title('Receiver Operating Characteristic')
plt.legend(loc="lower right")
plt.show()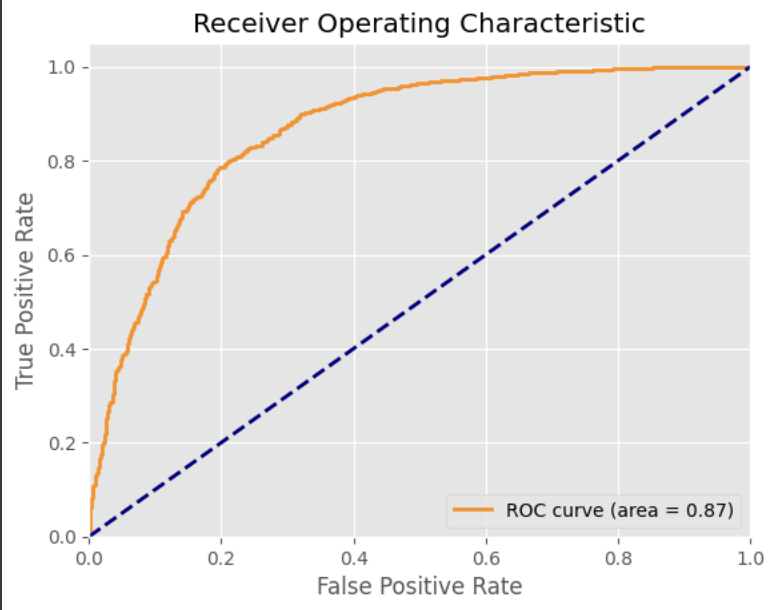
점선 : 찍어도 나오는 수치
실선 : 평가값
area = 노란색 실선을 포함하는 면적 (-> 클수록 좋음)
# prompt: 모델의 학습 결과 저장
import pandas as pd
from sklearn.metrics import accuracy_score, precision_score, recall_score, f1_score, roc_auc_score
# 모델의 학습결과 저장
results = pd.DataFrame(columns=['Model Name','Accuracy','Precision Score','Recall Score','F1-Score','roc_auc'])
y_pred = model_lr.predict(X_test)
model_result = ['Linear Regression',accuracy_score(y_test,y_pred),
precision_score(y_test,y_pred), recall_score(y_test,y_pred),
f1_score(y_test,y_pred),roc_auc_score(y_test,y_pred)]
results.loc[len(results)]=model_result
results
분류 모델의 성능 평가 지표
F1 Score
- 정밀도와 재현율의 조화평균. 균형을 고려한다.
- F1 Score = 2 x 𝑃𝑟𝑒𝑐𝑖𝑠𝑖𝑜𝑛∗𝑅𝑒𝑐𝑎𝑙𝑙 / 𝑃𝑟𝑒𝑐𝑖𝑠𝑖𝑜𝑛+𝑅𝑒𝑐𝑎𝑙𝑙
- 값이 클수록 모델의 성능이 좋음을 의미
ROC curve (Receiver Operating Characteristic Curve)
- 분류 모델의 성능을 다양한 임계값에서 시각적으로 평가하는 그래프
- X축 : FPR (False Positive Rate). 거짓 양성 비율.
✓ 실제 음성인데 양성으로 잘못 예측한 비율
✓ 𝐹𝑃𝑅 = 𝐹𝑃 𝐹𝑃+𝑇𝑁
- Y축 : TPR (True Positive Rate). 진짜 양성 비율
✓ 실제 양성인데 모델이 양성으로 잘 예측한 비율
✓ 𝑇𝑃𝑅 = 𝑇𝑃 𝑇𝑃+𝐹N
AUC (Area Under the Curve)
- ROC 곡선 아래의 면적으로, 모델의 분류 능력을 나타냄
✓ 1: 완벽한 모델
✓ 0.5 : 랜덤 추측과 동일한 모델
✓ <0.5 : 랜덤 추측보다 못한 경우
모델 평가
▪️모델의 과적합 확인
학습데이터의 y값과 모델의 예측값을 이용하여 평가
테스트데이터의 y값과 모델의 예측값을 이용하여 평가
K-Nearest Neighbors, KNN 알고리즘
KNN알고리즘 기본 개념
새로운 데이터 포인트의 클래스나 값을 결정할 때, 가장 가까운 K개의 이웃 데이터 포인트를 참조하는 방식
✓ 학습 과정 없이 훈련 데이터에서 가장 가까운 K개의 이웃을 찾아 그들의 정보를 기반으로 분류나 회귀 수행
작동 방식
✓ 분류 : K개 이웃의 다수결로 클래스 결정
✓ 회귀 : K개 이웃의 목표 변수 평균으로 예측
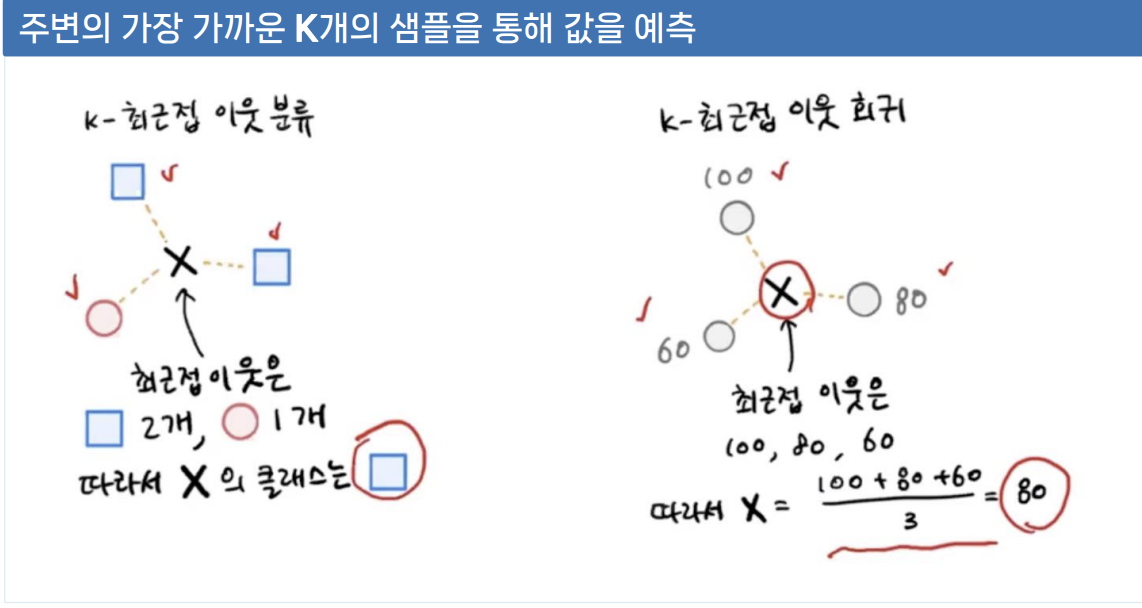
그림출처 : https://velog.io/@happyhillll/혼공-6장-회귀-문제-이해-k-최근접-이웃-알고리즘으로-풀어보기
[혼공] 6장 회귀 문제 이해, k-최근접 이웃 알고리즘으로 풀어보기
이전과 다르게 stratify는 지정하지 않음 : target은 예측값이기 때문에.stratify는 데이터의 개수가 작을경우 반드시 써야함.prach_length : 1차원 배열이기 때문에 train_input, test_input 모두 1차원 배열로 나
velog.io
거리측정
✓ 주로 유클리드 거리 사용
✓ 다른 거리 측정법(맨해튼, 민코프스키 등)도 가능
• K값 선택
✓ 홀수 선택 (분류 시 동점 방지)
✓ 작은 K : 과적합 위험. 노이즈에 민감
✓ 큰 K : 과소적합 위험 ▪️KNN알고리즘 개념
• 장점
✓ 단순성 : 구현이 간단하고 이해하기 쉬움
✓ 훈련 과정이 빠름
• 단점
✓ 이상치에 민감 (피처 스케일링이 중요함)
✓ 피처의 중요도를 반영하지 않음
KNN알고리즘 분류
① 데이터 준비: 학습 데이터셋 준비. 각 데이터 포인트는 다차원 공간의 점으로 표현
② 거리 측정: 새로운 데이터 포인트가 주어지면, 학습 데이터셋의 각 데이터 포 인트와의 거리를 계산. 거리 측정을 위해 주로 유클리드 거리(Euclidean Distance)를 사용하지만, 맨해튼 거리(Manhattan Distance)나 다른 거 리 측정 방법을 사용할 수도 있다.
③ K개의 이웃 선택: 계산된 거리 중 가장 짧은 거리의 K개의 이웃을 선택
④ 다수결 투표: 선택된 K개의 이웃 중 가장 빈번하게 등장하는 클래스를 새로 운 데이터 포인트의 클래스로 결정 ※ 회귀의 경우 평균 계산: 선택된 K개의 이웃의 값을 평균 내어 새로운 데 이터 포인트의 값을 결정
거리 측정 방법
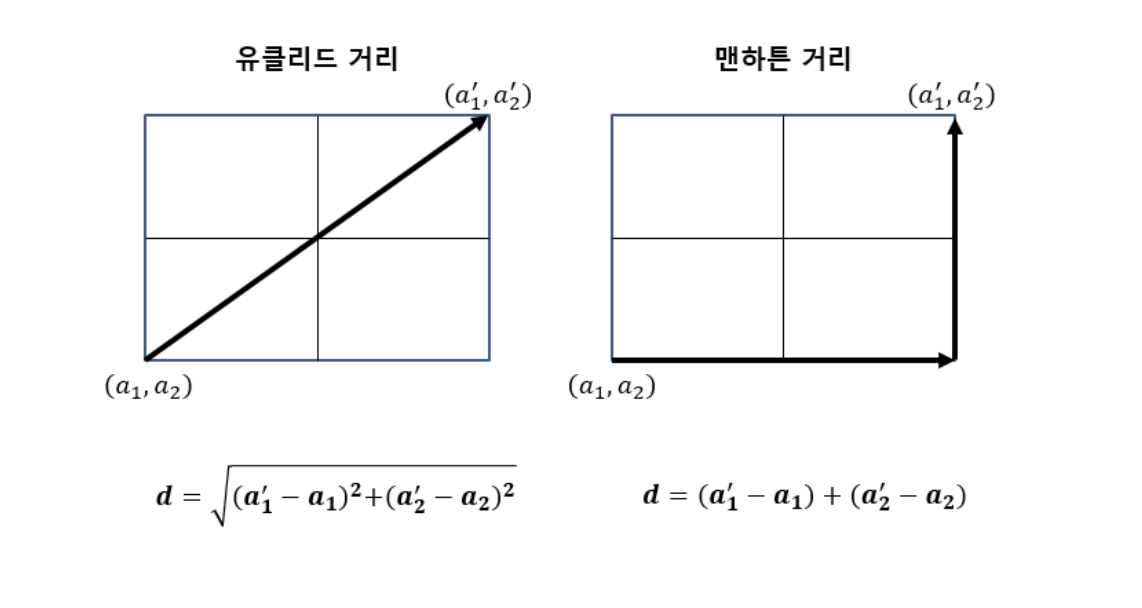
# prompt: 과적합 해결
import matplotlib.pyplot as plt
# KNN Classifier - 최적의 k 찾기
k_values = range(1, 21) # 1부터 20까지 k 값 테스트
train_scores = []
test_scores = []
for k in k_values:
model_knn = KNeighborsClassifier(n_neighbors=k)
model_knn.fit(X_train, y_train)
train_scores.append(model_knn.score(X_train, y_train))
test_scores.append(model_knn.score(X_test, y_test))
# 결과 시각화
plt.plot(k_values, train_scores, label='Train Accuracy')
plt.plot(k_values, test_scores, label='Test Accuracy')
plt.xlabel('k')
plt.ylabel('Accuracy')
plt.title('KNN Accuracy for Different k Values')
plt.legend()
plt.show()
# 최적의 k 값 선택 (테스트 정확도가 가장 높고 과적합이 적은 k)
optimal_k = test_scores.index(max(test_scores)) + 1 # 인덱스는 0부터 시작하므로 1 더함
print("Optimal k:", optimal_k)
# 최적의 k 값으로 모델 재학습 및 평가
best_model_knn = KNeighborsClassifier(n_neighbors=optimal_k)
best_model_knn.fit(X_train, y_train)
y_pred = best_model_knn.predict(X_test)
print("Test accuracy with optimal k:", accuracy_score(y_test, y_pred))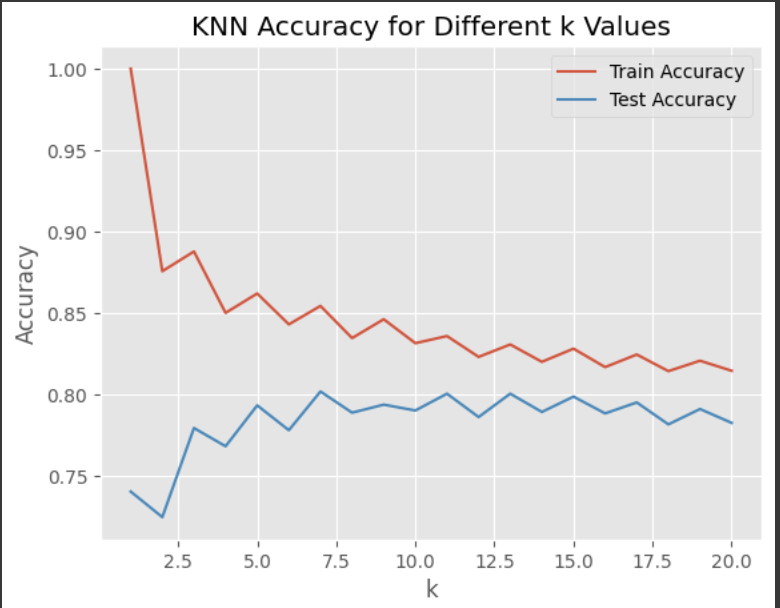

# prompt: 모델의 학습 결과 저장
y_pred = model_knn.predict(X_test)
model_result = ['KNN',accuracy_score(y_test,y_pred),
precision_score(y_test,y_pred), recall_score(y_test,y_pred),
f1_score(y_test,y_pred),roc_auc_score(y_test,y_pred)]
results.loc[len(results)]=model_result
results
Decision Tree (의사결정 트리)
▪️분류
• 데이터의 특성을 바탕으로 분기를 만들어 트리 구조로 의사결정 과정을 모델링하는 방법
▪️회귀
분류트리와 회귀트리
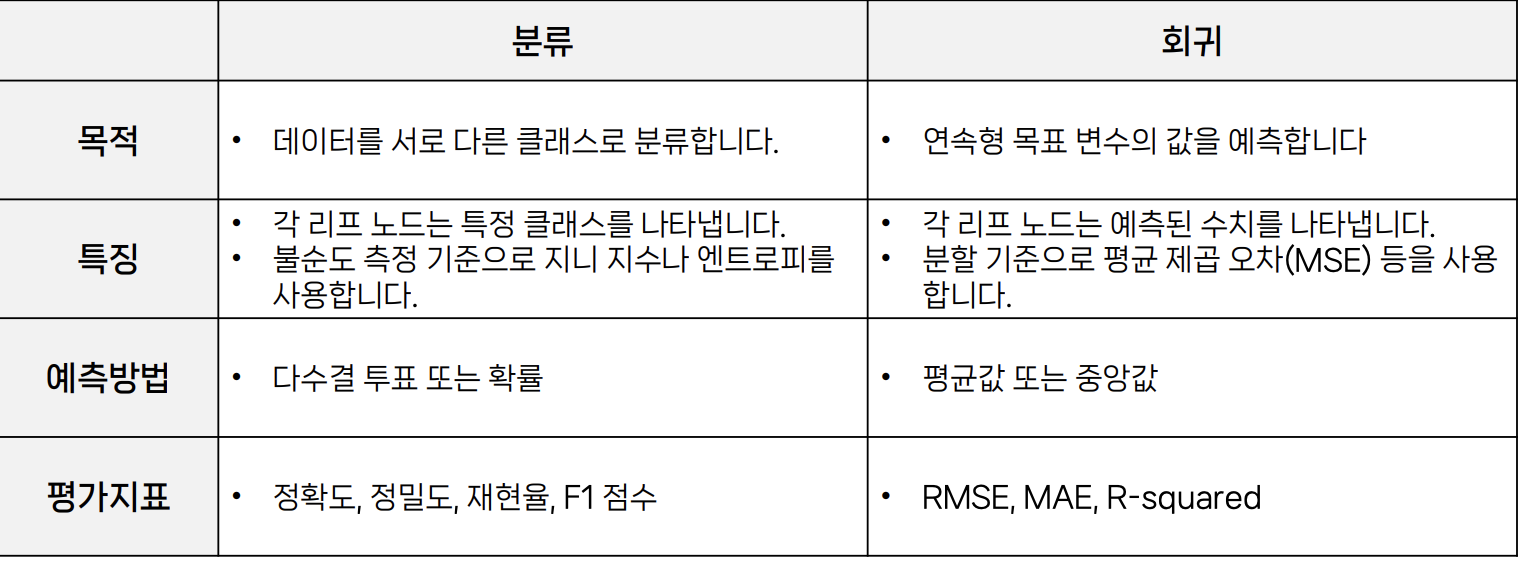
▪️의사결정트리의 장단점
장점
- 만들어진 모델을 시각화하여 모델이 어떻게 훈련 되었는지 해석하기 쉽니다.
- 데이터의 스케일에 구애받지 않는다.
- 학습이 끝난 결정트리의 작업 속도가 빠르다.
단점
- 과적합이 되는 경향이 있어 모델의 일반화 성능이 좋지 않은 편이다.
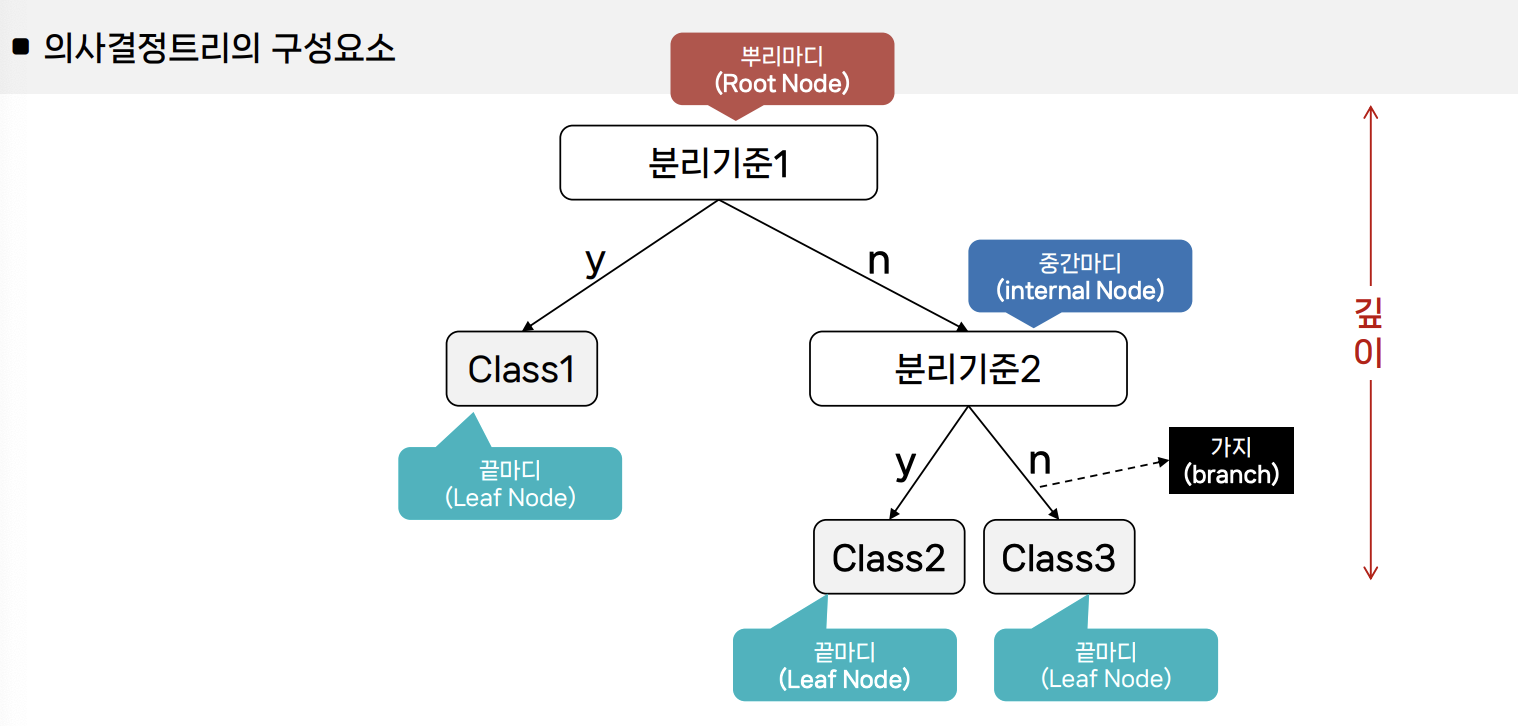
▪️데이터 분할 기준 : 지니불순도(Gini Impurity)
- 의사결정트리에서 데이터의 불순도, 즉 섞임 정도를 측정하는 지표
- 노드에서 무작위로 선택된 샘플이 잘못 분류될 확률을 나타냄
- 데이터가 얼마나 다양하게 섞여있는지, 또는 특정 클래스가 얼마나 혼합되어 있는지를 평가하는 데 사용

- 지니불순도의 최솟값 : 0
- 지니불순도의 최댓값 ∶ 1 − 1 𝑛 (클래스가 2개일 때 0.5, 3개일 때 0.667, 4개일 때 0.75, …)
▪️분류된 값이 순도가 높아지도록(불순도가 낮아지도록) 분기
▪️의사결정트리 알고리즘
CART
의사결정트리를 만들기 위한 매우 일반적이고 널리 사용되는 알고리즘 • 이진 분할(binary split)을 사용하여 데이터를 분할한다. • 분류 문제에서는 지니 불순도(Gini Impurity), 회귀 문제에서는 평균 제곱 오차(Mean Squared Error)를 최소화하는 방향으로 분할 기준을 선택한다. • 가지치기를 통해 트리의 복잡성을 조절한다. • 사이킷런의 의사결정트리 구현은 CART 알고리즘을 기반으로 한다.
CHAID
Chi-squared Automatic Interaction Detector
• 카이제곱 통계량을 사용하여 데이터를 분할하는 알고리즘
• 주로 범주형 데이터에 사용되며, 연속형 데이터를 처리하기 위해서는 이를 범주형으로 변환해야 한다.
• 데이터를 분할할 때 부모와 자식 노드 간의 통계적 유의성을 평가하여 최적의 분할을 선택한다.
▪️가지치기(Pruning)
목적 : 트리의 복잡성 감소, 과적합(Overfitting) 방지, 일반화 성능 향상
주요 parameter'
max_depth : 트리의 최대 깊이 규정. 깊이가 깊어지면 과적합 문제가 발생할 수 있으므로 제어 필요
min_sample_split : 노드를 분할하기 위한 최소한의 샘플 데이터 수(과적합 제어)
min_sample_leaf : leaf(밑단 노드)가 되기 위한 최소한의 데이터 수
max_features : 최적의 분할을 위해 고려할 최대 피처 개수
max_leaf_nodes : leaf의 최대 개수
• 과도한 가지치기는 underfitting을 발생
▪️데이터를 여러 구간으로 나누고, 각 구간에 대해 예측 값을 계산하여 입력 데이터에 대응하는 출력을 제공
분할 기준
✓ 주로 MSE(Mean Squared Error)를 최소화하는 방향으로 분할
✓ 분산 감소(Variance Reduction)을 목표로 한다. • 예측 방법
✓ 새로운 데이터 포인트가 속하는 리프 노드의 평균값을 예측값으로 사용
• 장점 ✓ 비선형 관계를 모델링할 수 있다.
✓ 특성의 중요도를 쉽게 해석할 수 있다.
✓ 전처리(예:정규화)가 거의 필요 없다.
• 단점
✓ 과적합의 가능성이 있다.
✓ 연속적인 출력보다는 계단 함수 형태의 예측을 한다.
# 모델 생성 및 훈련
from sklearn.tree import DecisionTreeClassifier
model_dt = DecisionTreeClassifier()
model_dt.fit(X_train, y_train)
# 모델 평가
print("test accuracy:", model_dt.score(X_test, y_test))
print("train accuracy:", model_dt.score(X_train, y_train))
#test accuracy: 0.7586206896551724
#train accuracy: 1.0
# prompt: decisiontree 과적합 해결
# Decision Tree Classifier with Hyperparameter Tuning
from sklearn.model_selection import GridSearchCV
# 모델 생성
model_dt = DecisionTreeClassifier()
# 하이퍼파라미터 튜닝을 위한 그리드 설정
param_grid = {
'max_depth': [3, 5, 7, 10],
'min_samples_split': [2, 5, 10],
'min_samples_leaf': [1, 2, 4]
}
# GridSearchCV를 사용하여 최적의 하이퍼파라미터 찾기
grid_search = GridSearchCV(model_dt, param_grid, cv=5)
grid_search.fit(X_train, y_train)
# 최적의 하이퍼파라미터 출력
print("Best hyperparameters:", grid_search.best_params_)
# 최적의 모델
best_model_dt = grid_search.best_estimator_
# 모델 평가
print("test accuracy:", best_model_dt.score(X_test, y_test))
print("train accuracy:", best_model_dt.score(X_train, y_train))
#Best hyperparameters: {'max_depth': 7, 'min_samples_leaf': 4, 'min_samples_split': 2}
#test accuracy: 0.8150470219435737
#train accuracy: 0.8413036174263635
# 모델의 학습 결과 시각화
import matplotlib.pyplot as plt
from sklearn import tree
plt.figure(figsize=(15, 10))
tree.plot_tree(best_model_dt, max_depth=2, feature_names=X_preprocessed.columns, class_names=['No', 'Yes'], filled=True)
plt.show()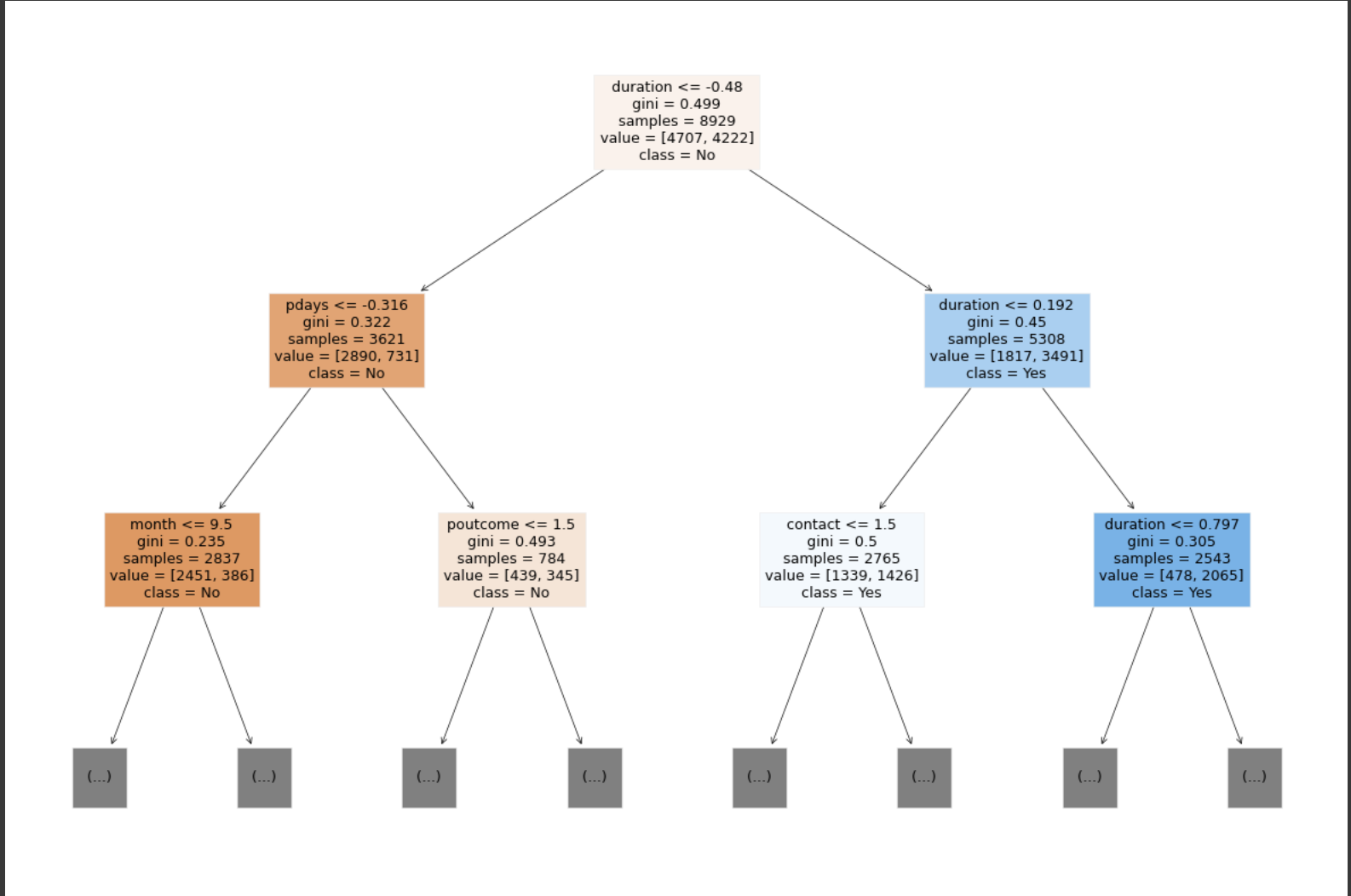
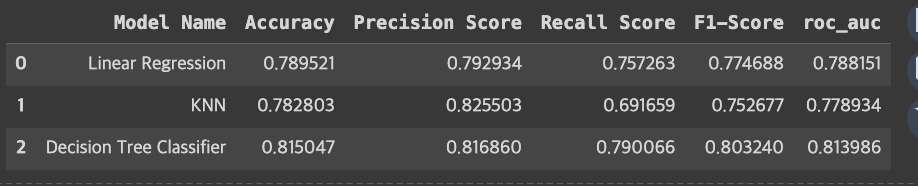
# 모델의 학습결과 저장
y_pred = best_model_dt.predict(X_test)
model_result = ['Decision Tree Classifier',accuracy_score(y_test,y_pred),
precision_score(y_test,y_pred), recall_score(y_test,y_pred),
f1_score(y_test,y_pred),roc_auc_score(y_test,y_pred)]
results.loc[len(results)]=model_result
results
앙상블 모델
Random Forest
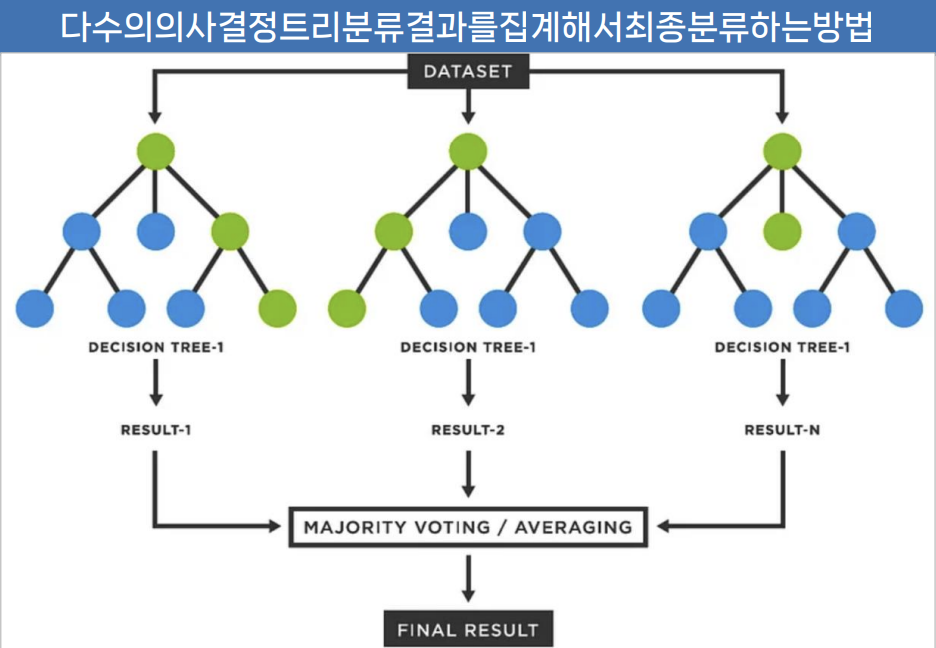
여러 개의 의사결정트리(Dicision Tree)를 앙상블(ensemble) 방식으로 결합하여 예측 성능을 향상시키는 기법
배깅(Bootstrap Aggregation)
✓ 원래의 학습 데이터셋에서 여러 개의 중복을 허용하는 부트스트랩 샘플(무작위 샘플)을 생성
✓ 각 부트스트랩 샘플을 사용하여 개별 트리 학습
랜덤 피처 선택(Random Feature Selection)
✓ 각 트리의 노드 분할 시 모든 피처를 고려하지 않고, 무작위로 선택된 피처의 서브셋만을 사용
✓ 이를 통해 트리 간의 상관성을 줄이고, 모델의 다양성을 증가
앙상블(Ensemble) 방식
✓ 분류 문제에서는 다수결(Majority Voting)을 통해 최종 예측 클래스를 결정
✓ 회귀 문제에서는 개별 트리의 평균 예측값을 사용하여 최종 예측
장점
✓ 강력한 성능 : 단일 트리보다 더 높은 예측 성능
✓ 과적합 방지 : 배깅과 랜덤 피처 선택으로 인해 모델이 훈련 데이터에 과적합 되지 않고, 일반화 성능이 뛰어남
✓ 변수 중요도 : 각 피처의 중요도를 계산하여, 예측에 가장 큰 영향을 미치는 피처를 선택할 수 있음
✓ 견고성 : 노이즈나 일부 결측치에 강하며, 트리의 개수가 많아질수록 모델의 성능이 안정화 됨
단점
✓ 복잡성 : 많은 수의 트리를 사용하기 때문에, 모델이 복잡해지고 해석이 어려울 수 있음
✓ 훈련시간 : 개별트리의 수가 많아질수록 학습 시간이 길어짐
하이퍼파라미터
✓ n_estimators : 생성할 트리의 수
✓ 개별 트리에 대해서는 단일트리의 하이퍼라미터와 동일
# 모델 생성 및 훈련
from sklearn.ensemble import RandomForestClassifier
model_rf = RandomForestClassifier()
model_rf.fit(X_train, y_train)
# 모델 평가
print("test accuracy:", model_rf.score(X_test, y_test))
print("train accuracy:", model_rf.score(X_train, y_train))
#test accuracy: 0.8343036274070756
#train accuracy: 1.0
#과적합 발생
# prompt: RandomizedSearchCV로 최적화해줘.
from sklearn.model_selection import RandomizedSearchCV
# 모델 생성
model_rf = RandomForestClassifier()
# 하이퍼파라미터 튜닝을 위한 그리드 설정
param_dist = {
'n_estimators': [50, 100, 200],
'max_depth': [None, 10, 20, 30],
'min_samples_split': [2, 5, 10],
'min_samples_leaf': [1, 2, 4]
}
# RandomizedSearchCV를 사용하여 최적의 하이퍼파라미터 찾기
random_search = RandomizedSearchCV(model_rf, param_distributions=param_dist, n_iter=10, cv=5)
random_search.fit(X_train, y_train)
# 최적의 하이퍼파라미터 출력
print("Best hyperparameters:", random_search.best_params_)
# 최적의 모델
best_model_rf = random_search.best_estimator_
# 모델 평가
print("test accuracy:", best_model_rf.score(X_test, y_test))
print("train accuracy:", best_model_rf.score(X_train, y_train))
#Best hyperparameters: {'n_estimators': 200, 'min_samples_split': 10, 'min_samples_leaf': 1, 'max_depth': None}
#test accuracy: 0.8307210031347962
#train accuracy: 0.9445626609922724# 모델의 학습결과 저장
y_pred = best_model_rf.predict(X_test)
model_result = ['RandomFroest Classifier',accuracy_score(y_test,y_pred),
precision_score(y_test,y_pred), recall_score(y_test,y_pred),
f1_score(y_test,y_pred),roc_auc_score(y_test,y_pred)]
results.loc[len(results)]=model_result
results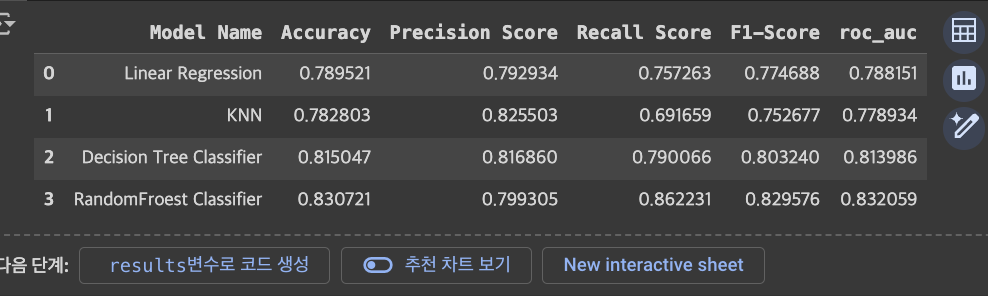
Gradient Boosting
▪️Gradient Boosting 기본 개념
- Boosting 모델 : 일련의 학습기들을 순차적으로 학습시키며, 각 학습기는 이전 학습기들의 오류를 보정하는 방식으로 학습
- Gradient Boosting은 손실 함수(loss function)의 그래디언트를 따라 각 학습기를 학습시키는 것이 특징
- 회귀와 분류 모델에 모두 사용할 수 있다.
- 성능이 뛰어나다
변형 모델
✓ XGBoost (Extreme Gradient Boosting): 정규화, 병렬처리 등 최적화 기능 추가
✓ LightGBM (Light Gradient Boosting Machine): 더 빠른 학습 속도, 큰 데이터셋에 효과적
✓ CatBoost: 범주형 변수 처리 개선, 오버피팅 방지 기법 포함
① 초기 모델 생성: 학습을 시작하기 위해 간단한 모델(일반 적으로 평균값)을 생성합니다.
② 잔여 오차(residual error) 계산: 현재 모델의 예측값과 실제 값 사이의 잔여 오차를 계산합니다.잔여 오차에 대 한 새로운
③ 모델 학습: 잔여 오차를 예측하도록 새로운 학습기를 학 습시킵니다.
④ 모델 업데이트: 학습된 모델을 현재 모델에 추가합니다.
⑤ 반복: 지정된 횟수만큼 또는 오차가 충분히 작아질 때까 지 2~4 과정을 반복합니다.
# XGBoost
!pip install xgboost
from xgboost import XGBClassifier
# 모델 생성 및 훈련
model_xgb = XGBClassifier()
model_xgb.fit(X_train, y_train)
# 모델 평가
print("test accuracy:", model_xgb.score(X_test, y_test))
print("train accuracy:", model_xgb.score(X_train, y_train))
#test accuracy: 0.8423645320197044
#train accuracy: 0.9618098331280098
# 모델의 학습결과 저장
y_pred = model_xgb.predict(X_test)
model_result = ['XGBoost',accuracy_score(y_test,y_pred),
precision_score(y_test,y_pred), recall_score(y_test,y_pred),
f1_score(y_test,y_pred),roc_auc_score(y_test,y_pred)]
results.loc[len(results)]=model_result
results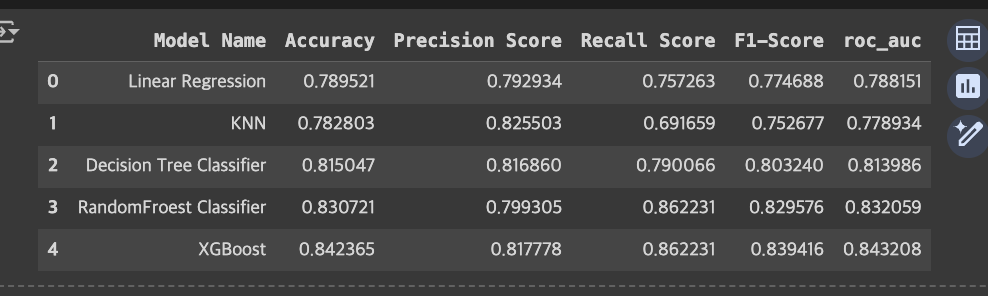
Naïve Bayes Classification
▪️Naïve Bayes 분류기의 개념 및 가정
개념 : Bayes 정리를 기반으로 한 확률적 분류 알고리즘
✓ 조건부 확률 : 다른 이벤트가 발생했을 때 어떤 이벤트가 발생할 확률.
✓ P(Y|X) = 𝑃(𝑋 𝑎𝑛𝑑 𝑌) / 𝑃(𝑋)
Naive한 가정 : 모든 특징(feature)들이 서로 독립적이며, 모든 특징들이 결과에 동등하게 기여한다.
✓ 각 특징에 대해 독립적으로 확률을 계산한 후 이를 결합하여 최종 확률을 산출한다.
✓ 장점 : 특징(feature)이 너무 많은 경우 특징간의 연관관계를 모두 고려하게 되면 너무 복잡해지는 경향이 있다. 특징 (feature)들이 서로 독립이라는 가정으로 분류를 쉽고 빠르게 할 수 있다.
✓ 단점 : 독립성 가정은 현실에서 항상 성립하지는 않으며, 이 가정에 위반되는 경우 에러를 발생시킬 수 있다.
▪️Bayes 추정
추론 대상의 사전 확률과 추가적인 정보를 기반으로 해당 대상의 사후 확률을 추론하는 통계적 방법
✓ 사전확률 : 사건이 발생하기 전에 이미 알고 있는 사건의 확률
✓ 사후확률 : 어떤 증거가 주어졌을 때, 그 증거를 바탕으로 사건이 발생할 확률
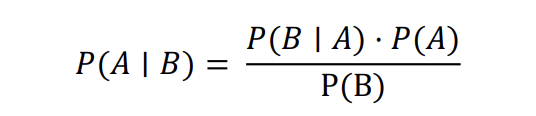
추론 대상의 사전 확률과 추가적인 정보를 기반으로 해당 대상의 사후 확률을 추론하는 통계적 방법
✓ 사전확률 : 사건이 발생하기 전에 이미 알고 있는 사건의 확률 (label만으로 구할 수 있는 확률)
✓ 사후확률 : 어떤 증거가 주어졌을 때, 그 증거를 바탕으로 사건이 발생할 확률
어떤 사람이 양성 판정을 받았을 때, 이 사람이 암환자일 확률은?
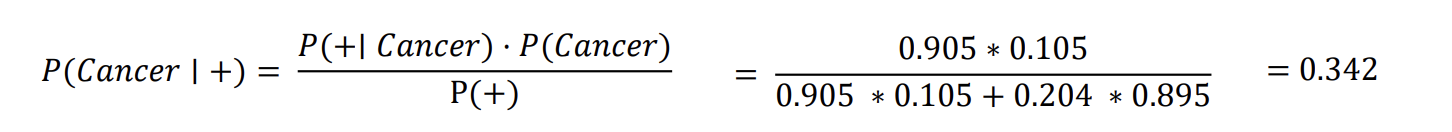
✓ 양성 판정을 받을 활률 P (+)
= 암환자가 양성판정을 받을 확률 + 암이 아닌 환자가 양성판정을 받을 확률 = 𝑃 + 𝐶 ∗ 𝑃 𝐶 + 𝑃 + ~𝐶 ∗ 𝑃(~𝐶) = 0.905 ∗ 0.105 + 0.204 ∗ 0.895 = 0.277605
응용분야
- 스팸메일 필터링 : 이메일의 단어를 특징으로 하여 스팸인지 아닌지 분류
- 감성분석 : 텍스트데이터의 단어를 특징으로 하여 감정(긍정,부정,중립 등)을 분석
- 문서분류 : 텍스트데이터의 단어를 특징으로 하여 뉴스기사, 논문 등을 주제별로 분류
- 의료진단 : 증상에 다른 질병 예측
- 추천시스템 : 사용자 과거 행동 데이터 및 프로필 기반으로 선호할 만한 제품 추천
• 가우시안 나이브 베이즈 (Gaussian Naive Bayes)
✓ 연속형 데이터에 사용, 특성이 정규 분포를 따른다고 가정. 각 특징의 평균과 분산을 사용하여 조건부 확률을 계산.
✓ 응용: 실수값 특성을 가진 데이터 분류
• 다항 나이브 베이즈 (Multinomial Naive Bayes)
✓ 이산형 데이터에 사용, 특성이 다항 분포를 따른다고 가정. 특정 클래스 내에서의 단어 빈도나 발생 횟수를 모델링
✓ 응용: 텍스트 분류, 문서 분류
• 베르누이 나이브 베이즈 (Bernoulli Naive Bayes)
✓ 이진 데이터에 사용, 특성이 베르누이 분포를 따른다고 가정. 각 특징이 0 또는 1의 값을 가지며, 특정 클래스 내에서의 단 어 존재 여부를 모델링
✓ 응용: 텍스트 분류 (단어의 존재/부재만 고려)
• 보완 나이브 베이즈 (Complement Naive Bayes)
✓ 다항 나이브 베이즈의 변형, 불균형 데이터셋에 효과적
✓ 응용: 클래스 불균형이 심한 텍스트 분류 문제
• 범주형 나이브 베이즈 (Categorical Naive Bayes)
✓ 범주형 데이터에 사용
✓ 응용: 범주형 특성을 가진 데이터 분류
# prompt: Naive Bayes 모델 생성 및 훈련
from sklearn.naive_bayes import GaussianNB
# 모델 생성 및 훈련
model_nb = GaussianNB()
model_nb.fit(X_train, y_train)
# 모델 평가
print("test accuracy:", model_nb.score(X_test, y_test))
print("train accuracy:", model_nb.score(X_train, y_train))
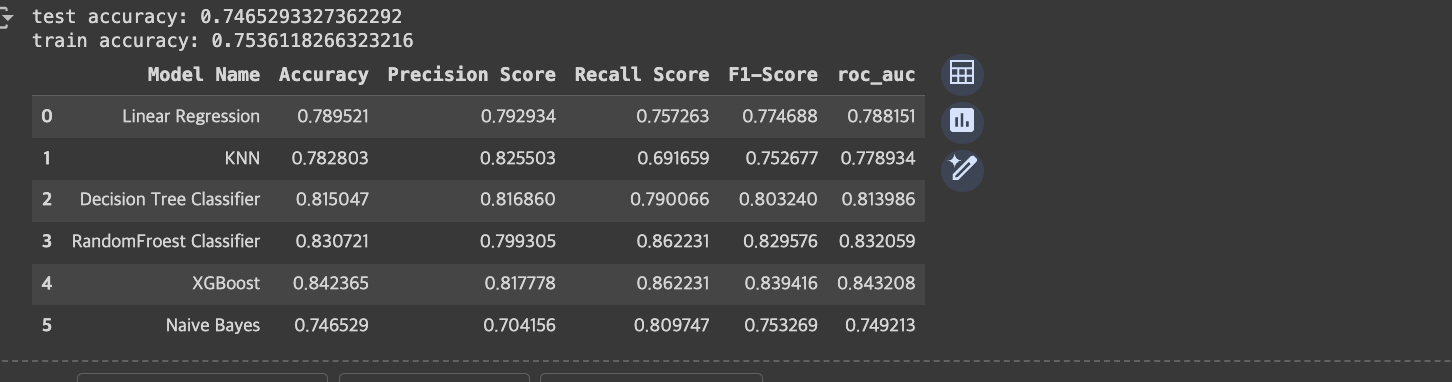
# 모델의 학습결과 저장
y_pred = model_nb.predict(X_test)
model_result = ['Naive Bayes',accuracy_score(y_test,y_pred),
precision_score(y_test,y_pred), recall_score(y_test,y_pred),
f1_score(y_test,y_pred),roc_auc_score(y_test,y_pred)]
results.loc[len(results)]=model_result
results
# 예측할 데이터
data = pd.DataFrame(
[[40,'admin.','married','tertiary','no',3000,'yes','no','cellular',5,'aug',1042,1,-1,0,'unknown'],
[19,'student','single','secondary','no',100,'no','no','unknown',1,'may',673,4,-1,0,'unknown'],
[35,'services','married','tertiary','yes',1000,'no','no','telephone',8,'jul',257,1,-1,0,'unknown']],
columns=X.columns
)
data
# 레이블 인코딩
data_preprocessed = data.copy()
for obj in objs:
le = encoders[obj]
data_preprocessed[obj] = le.transform(data[obj])
data_preprocessed
# 정규화
data_preprocessed[nums] = scaler.transform(data[nums])
data_preprocessed
# LogisticRegression으로 예측하기
y_pred = model_lr.predict(data_preprocessed)
y_pred_proba = model_lr.predict_proba(data_preprocessed)
print('예측결과(1:가입, 0:미가입):',y_pred)
print('정기예금에 가입할 확률:',y_pred_proba[:,1])
#예측결과(1:가입, 0:미가입): [1 1 0]
#정기예금에 가입할 확률: [0.96451957 0.68598855 0.33924705]
# knn으로 예측하기
y_pred = model_knn.predict(data_preprocessed)
y_pred_proba = model_knn.predict_proba(data_preprocessed)
print('예측결과(1:가입, 0:미가입):',y_pred)
print('정기예금에 가입할 확률:',y_pred_proba[:,1])
#예측결과(1:가입, 0:미가입): [1 0 0]
3정기예금에 가입할 확률: [0.8 0.15 0.15]
# Decision Tree로 예측하기
y_pred = best_model_dt.predict(data_preprocessed)
y_pred_proba = best_model_dt.predict_proba(data_preprocessed)
print('예측결과(1:가입, 0:미가입):',y_pred)
print('정기예금에 가입할 확률:',y_pred_proba[:,1])
#예측결과(1:가입, 0:미가입): [1 1 0]
#정기예금에 가입할 확률: [0.90196078 0.76506024 0.41617357]
# Random Forest로 예측하기
y_pred = best_model_rf.predict(data_preprocessed)
y_pred_proba = best_model_rf.predict_proba(data_preprocessed)
print('예측결과(1:가입, 0:미가입):',y_pred)
print('정기예금에 가입할 확률:',y_pred_proba[:,1])
#예측결과(1:가입, 0:미가입): [1 1 0]
#정기예금에 가입할 확률: [0.88424189 0.62458441 0.49814325]
# XGBoost로 예측하기
y_pred = model_xgb.predict(data_preprocessed)
y_pred_proba = model_xgb.predict_proba(data_preprocessed)
print('예측결과(1:가입, 0:미가입):',y_pred)
print('정기예금에 가입할 확률:',y_pred_proba[:,1])
#예측결과(1:가입, 0:미가입): [1 1 0]
#정기예금에 가입할 확률: [0.95011985 0.6929441 0.43498945]
03_공공자전거 수요 예측_실습
# 한글폰트 설치(실행 후 세션 다시 시작)
!pip install koreanize-matplotlib
# 라이브러리 임포트
import koreanize_matplotlib
import numpy as np
import pandas as pd
import matplotlib.pyplot as plt
import seaborn as sns
# 그래프 스타일 지정
plt.style.use('ggplot')
# 한글 폰트 테스트
pd.Series([-2,1,2]).plot(figsize=(4,2), title="한글폰트테스트")
plt.show()
# datetime 컬럼은 datetime 형식으로 읽어오도록 옵션 설정
df = pd.read_csv('https://raw.githubusercontent.com/JayoungKim-ai/ML_dataset/main/BikeSharingDemand.csv', parse_dates=['datetime'])
display(df.head(3))
display(df.tail(3))# 연, 월, 일, 시, 요일, 분기
df['year'] = df['datetime'].dt.year
df['month'] = df['datetime'].dt.month
df['day'] = df['datetime'].dt.day
df['hour'] = df['datetime'].dt.hour
df['dayofweek'] = df['datetime'].dt.dayofweek # 월요일:0, 일요일:6
df.head()
데이터탐색
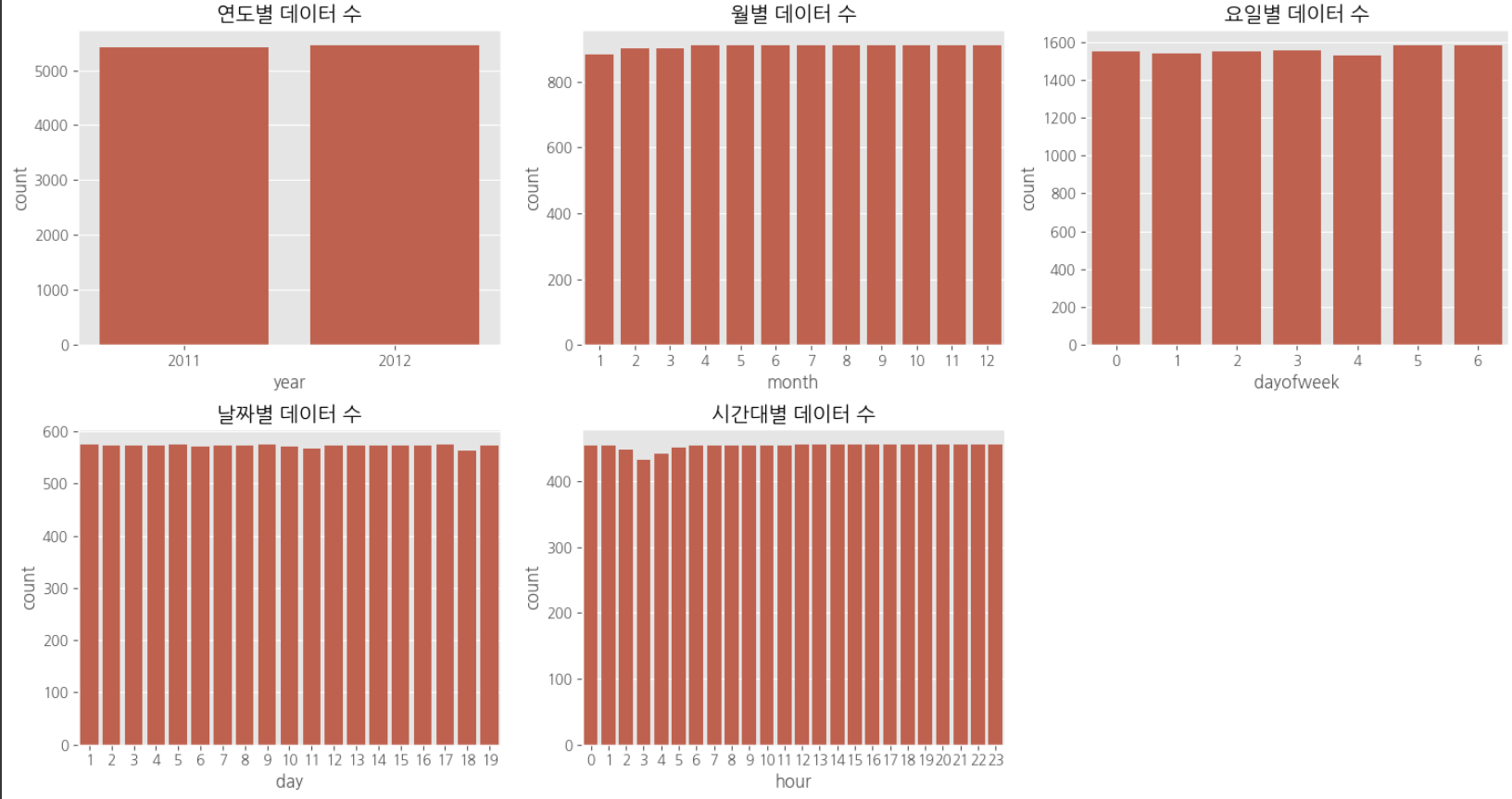
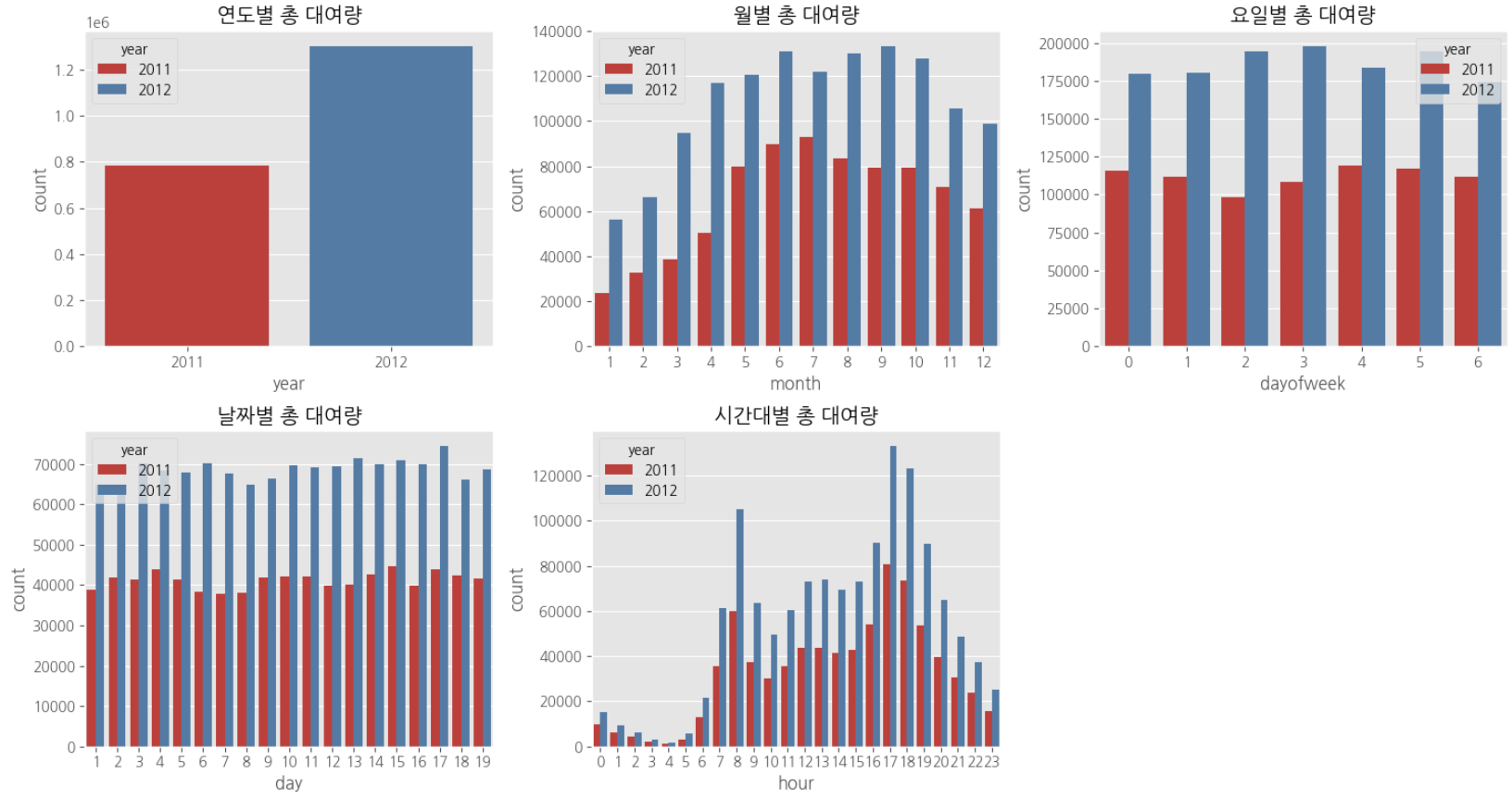
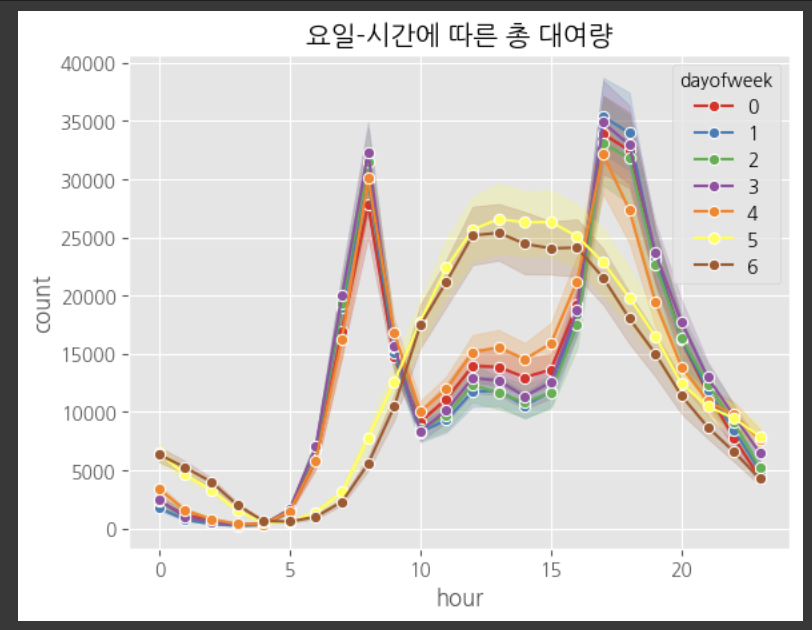
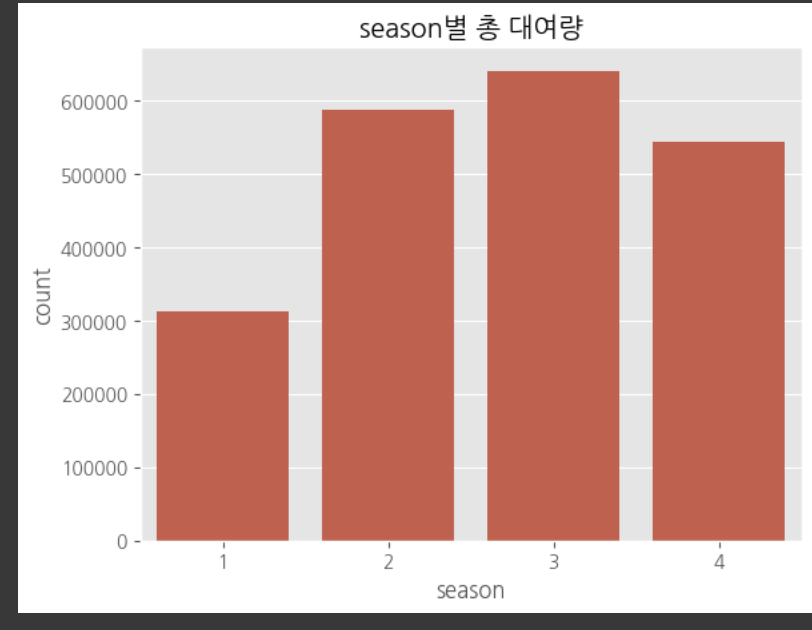
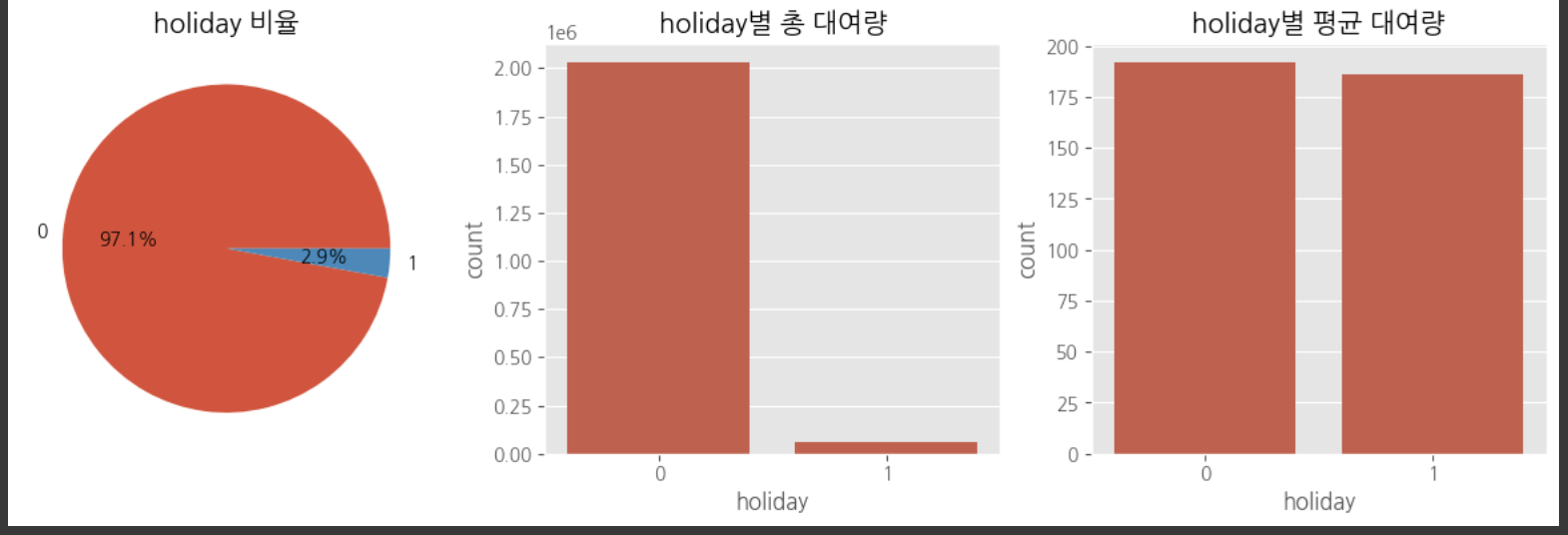
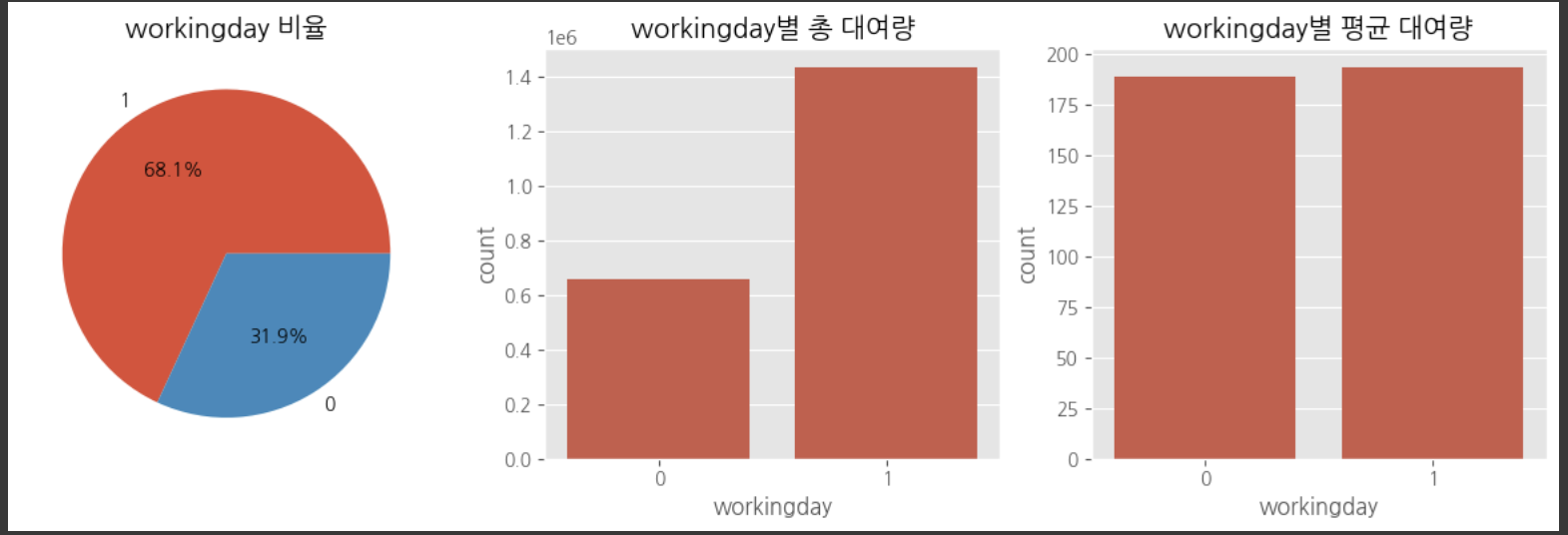
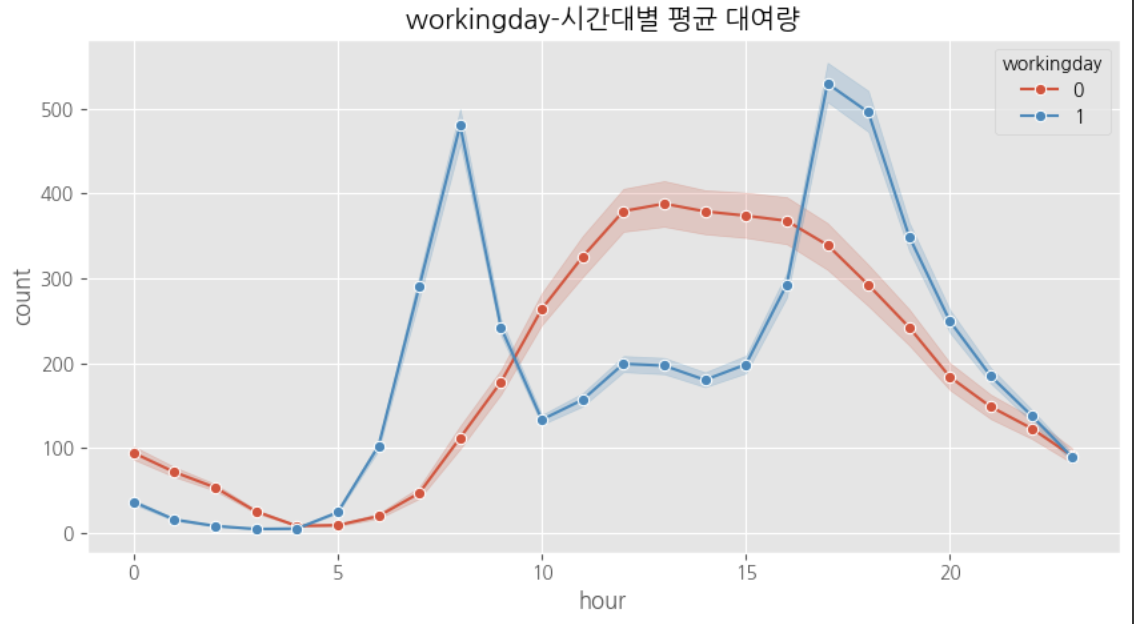
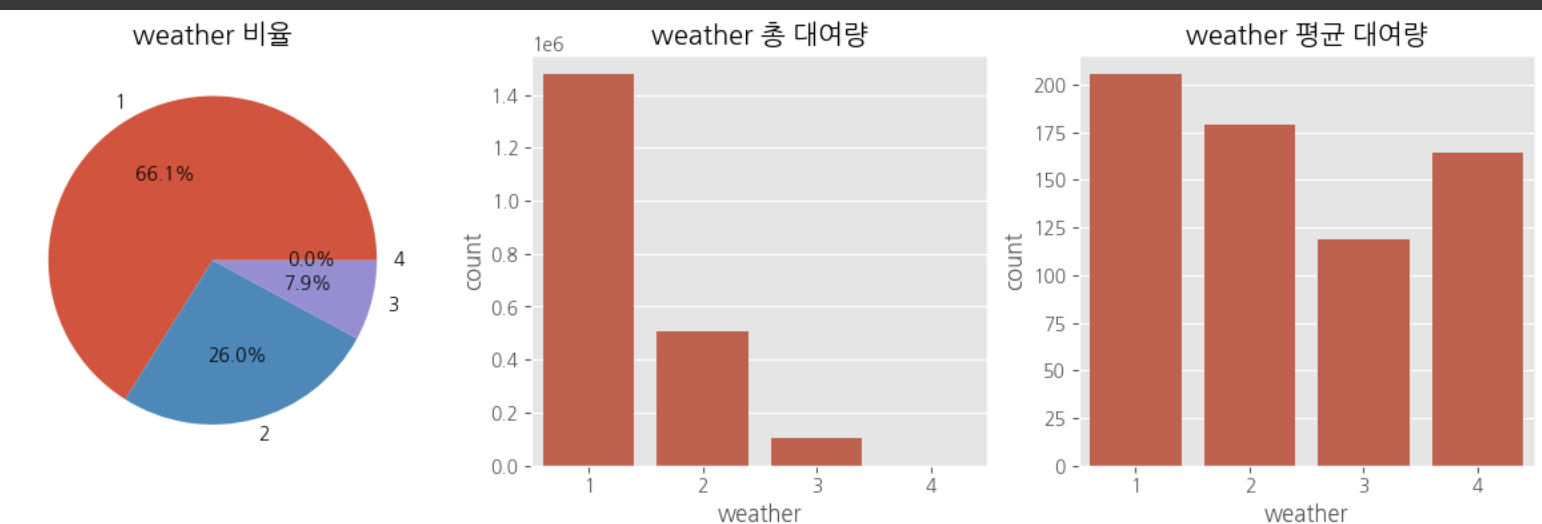
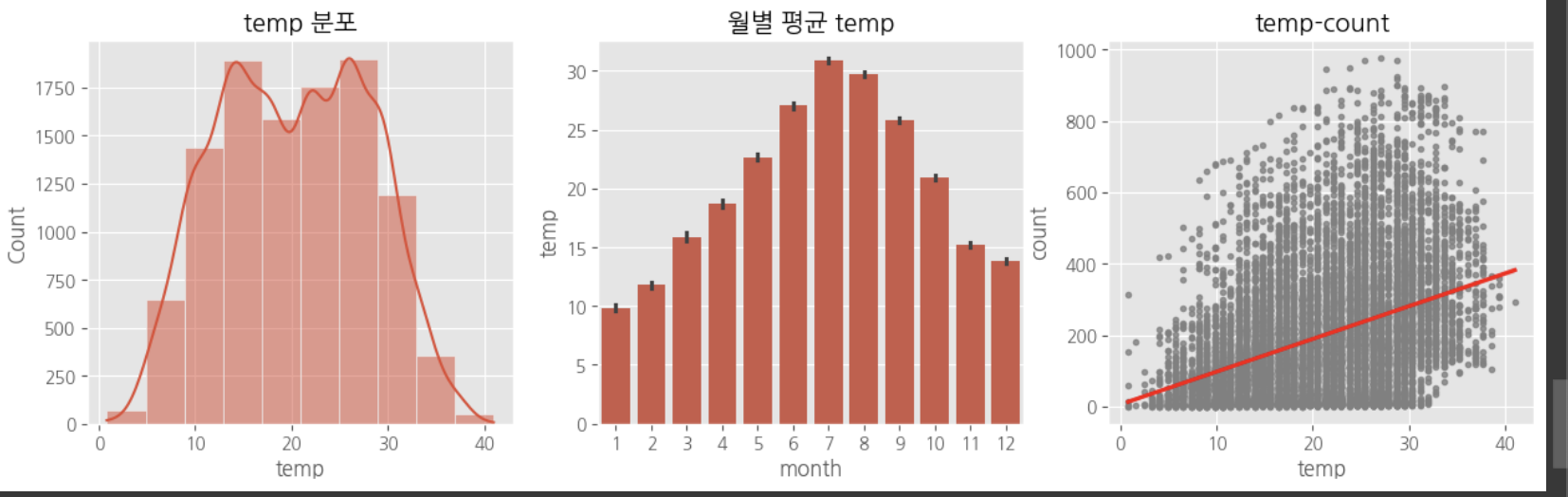
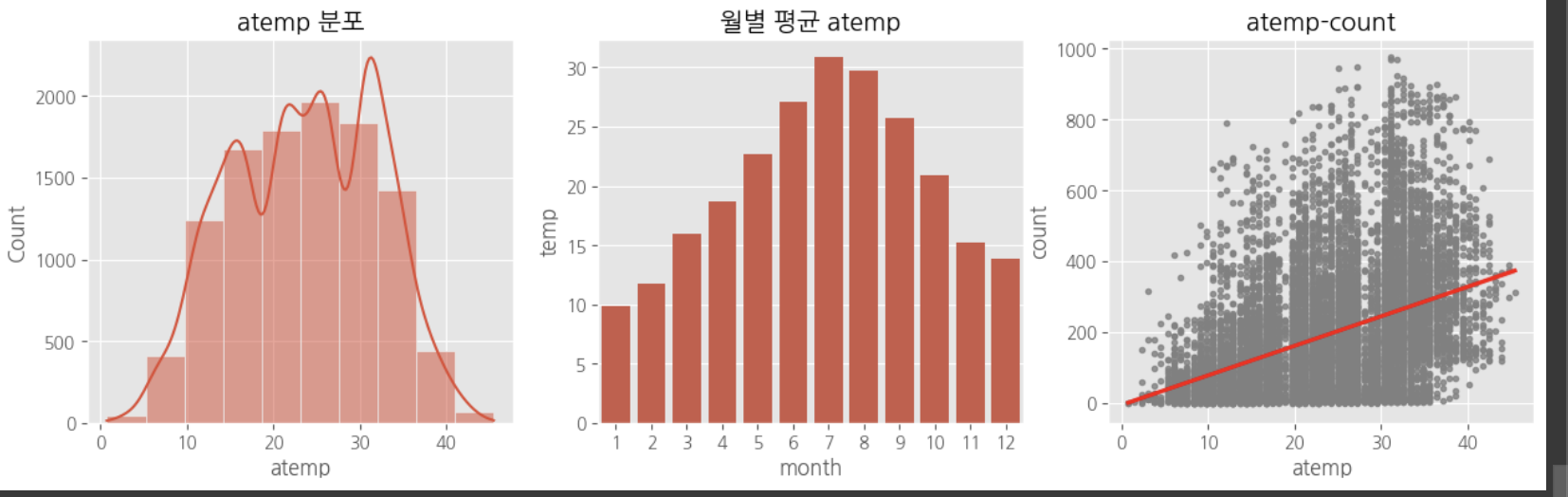
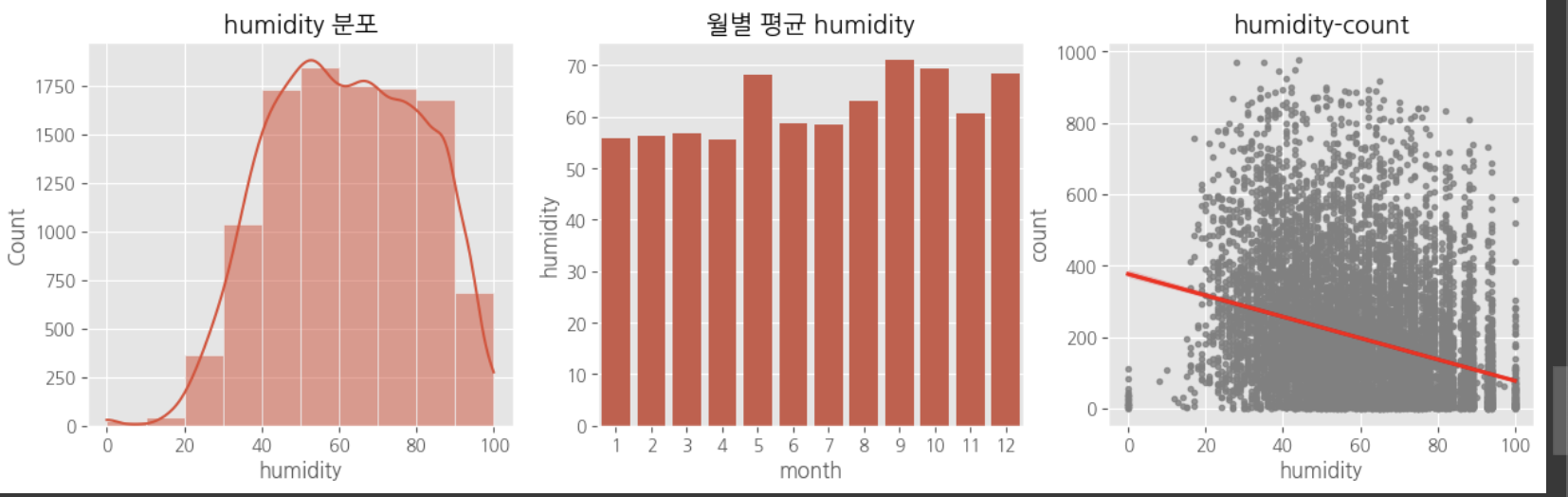
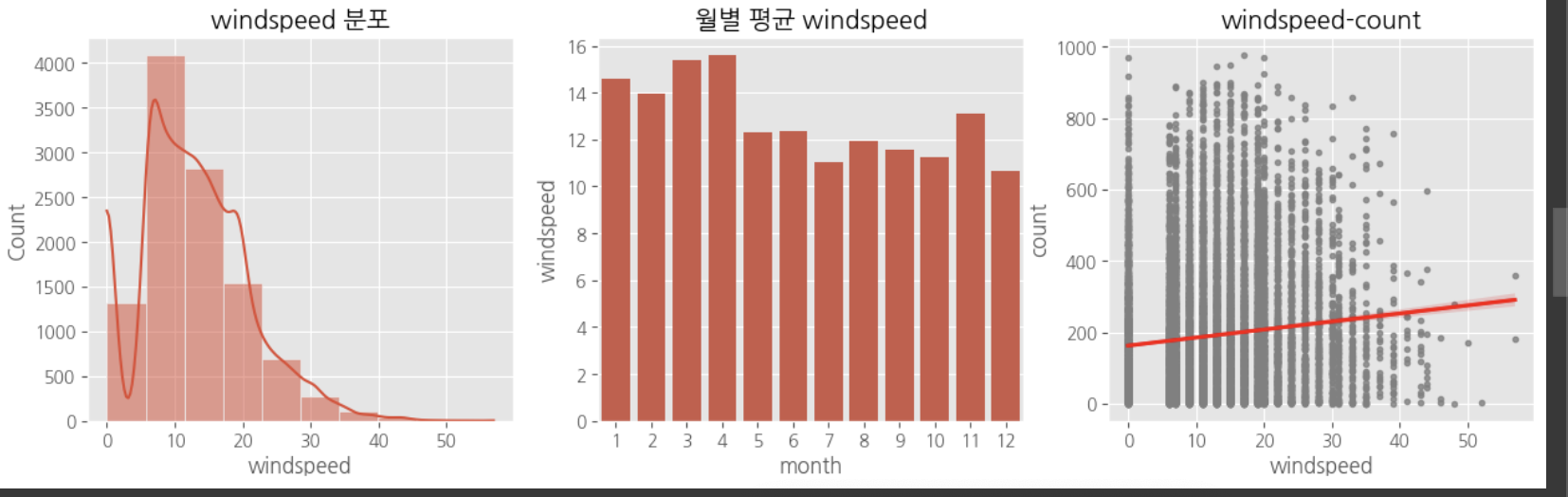
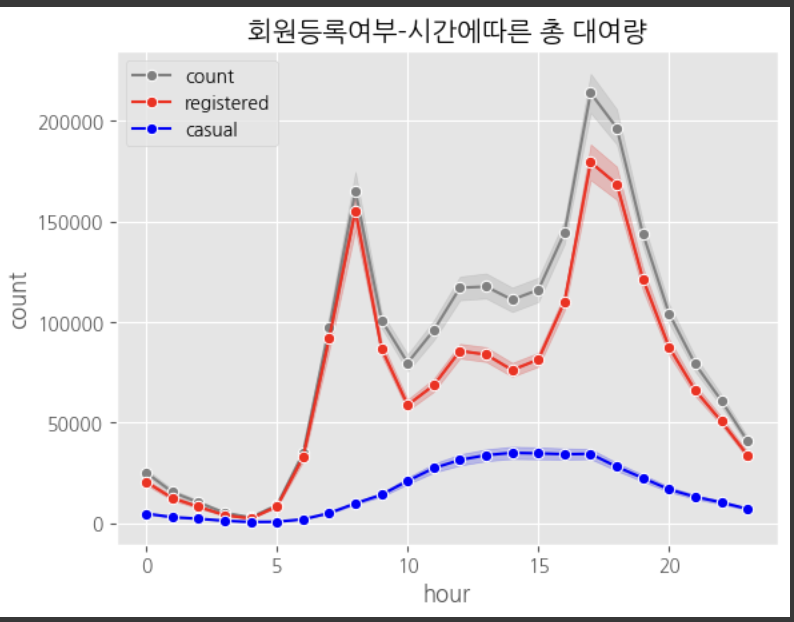
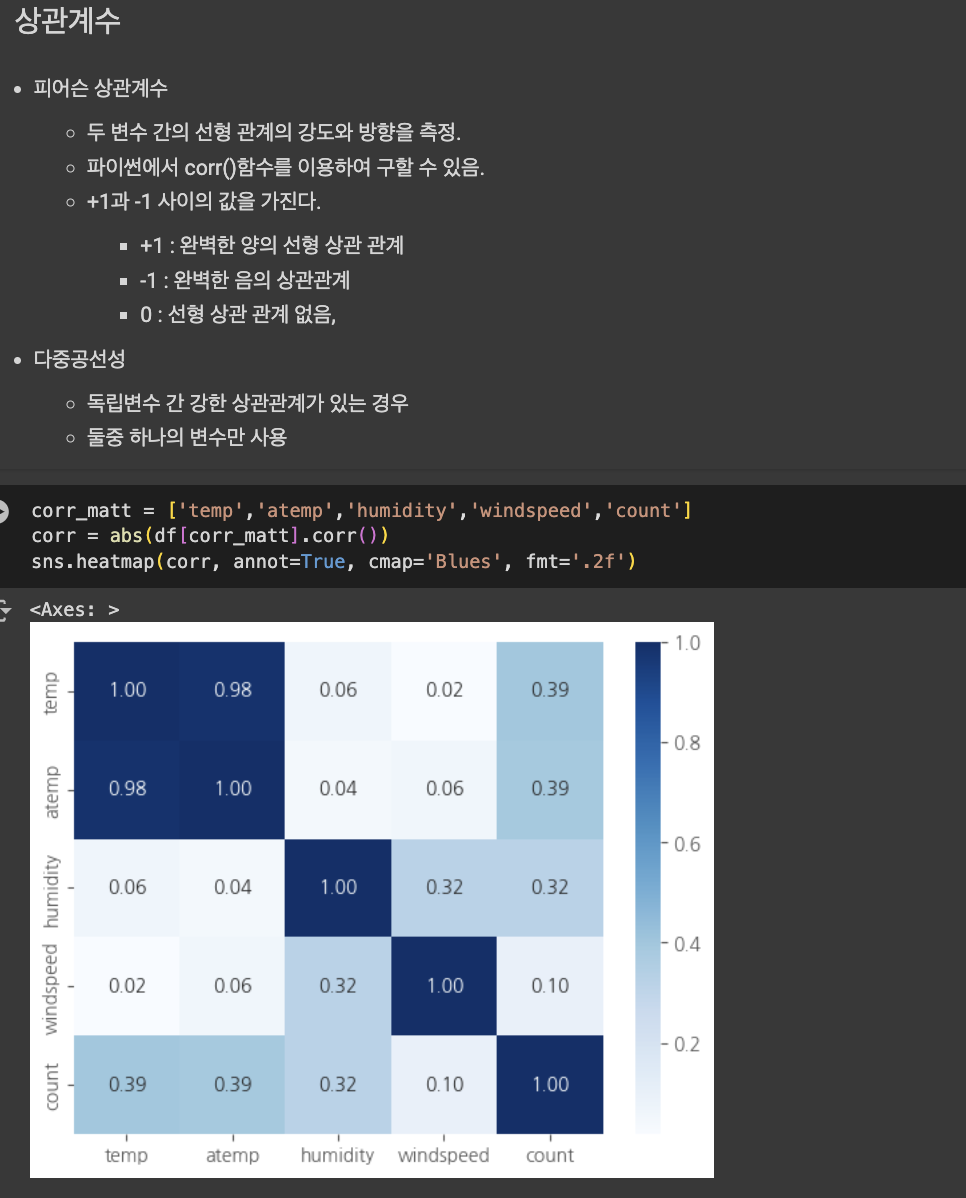
다중공산성 방지를 위하여 atemp, temp 중 하나의 변수만 선택

X = df[['holiday','workingday','weather','temp','humidity','windspeed','year','month','day','hour','dayofweek']].copy()
y = df['count'].copy()
#데이터 전처리
# 연속형 변수 스케일링
from sklearn.preprocessing import StandardScaler
scaler = StandardScaler()
X[['temp','humidity','windspeed']] = scaler.fit_transform(df[['temp','humidity','windspeed']])
X.head(3)
# year-2000
X['year'] = df['year']-2010
# 데이터 분할
from sklearn.model_selection import train_test_split
X_train, X_test, y_train, y_test = train_test_split(X, y, test_size=0.2, random_state=42)
X_train.shape, X_test.shape, y_train.shape, y_test.shape
from sklearn.linear_model import LinearRegression
# 모델 생성 및 훈련
model_lr = LinearRegression()
model_lr.fit(X_train, y_train)
# 과적합 확인
print('train:',model_lr.score(X_train, y_train))
print('test:',model_lr.score(X_test, y_test))
#train: 0.3858940229309653
#test: 0.39517692278681493
from sklearn.neighbors import KNeighborsRegressor
# 모델 생성 및 훈련
model_knn = KNeighborsRegressor()
model_knn.fit(X_train, y_train)
# 과적합 확인
print('train:',model_knn.score(X_train, y_train))
print('test:',model_knn.score(X_test, y_test))
#train: 0.8978743323339545
#test: 0.8357469724492553
from sklearn.tree import DecisionTreeRegressor
# 모델 생성 및 훈련
model_dt = DecisionTreeRegressor()
model_dt.fit(X_train, y_train)
# 과적합 확인
print('train:',model_dt.score(X_train, y_train))
print('test:',model_dt.score(X_test, y_test))
#train: 1.0
#test: 0.899884455809497
from sklearn.ensemble import RandomForestRegressor
# 모델 생성 및 훈련
model_rf = RandomForestRegressor()
model_rf.fit(X_train, y_train)
# 과적합 확인
print('train:',model_rf.score(X_train, y_train))
print('test:',model_rf.score(X_test, y_test))
#train: 0.9927365824898922
#test: 0.9532195060040306
# prompt: 최적의 모델 찾아줘.
from sklearn.model_selection import GridSearchCV
# 탐색할 매개변수 그리드 정의
param_grid = {
'n_estimators': [50, 100, 200],
'max_depth': [None, 10, 20],
'min_samples_split': [2, 5, 10]
}
# GridSearchCV 객체 생성
grid_search = GridSearchCV(estimator=RandomForestRegressor(), param_grid=param_grid, cv=5)
# 훈련 데이터에 그리드 검색 적용
grid_search.fit(X_train, y_train)
# 최적의 매개변수 출력
print("Best parameters: ", grid_search.best_params_)
# 최적의 모델 출력
best_model = grid_search.best_estimator_
print("Best model: ", best_model)
# 테스트 데이터에서 최적 모델의 성능 평가
print('test:', best_model.score(X_test, y_test))
#Best parameters: {'max_depth': None, 'min_samples_split': 2, 'n_estimators': 100}
#Best model: RandomForestRegressor()
#test: 0.9531235441726251
df_pred = pd.read_csv('https://raw.githubusercontent.com/JayoungKim-ai/ML_dataset/main/BikeSharingDemand_pred.csv',parse_dates=['datetime'])
df_pred.head()
# 연, 월, 일, 시, 요일 추가
df_pred['year'] = df_pred['datetime'].dt.year
df_pred['month'] = df_pred['datetime'].dt.month
df_pred['day'] = df_pred['datetime'].dt.day
df_pred['hour'] = df_pred['datetime'].dt.hour
df_pred['dayofweek'] = df_pred['datetime'].dt.dayofweek # 월요일:0, 일요일:6
# 컬럼 선택
X_pred = df_pred[['holiday','workingday','weather','temp','humidity','windspeed','year','month','day','hour','dayofweek']].copy()
# 연속형 변수 스케일링
X_pred[['temp','humidity','windspeed']] = scaler.transform(df_pred[['temp','humidity','windspeed']])
# year-2000
X_pred['year'] = df_pred['year']-2010
X_pred.head()
# 예측
y_pred = best_model.predict(X_pred)
df_pred['count'] = y_pred
df_pred.head()
# 예측결과 확인
sns.lineplot(data=df_pred, x='hour', y='count', marker='o', hue='dayofweek', palette='Set1')
plt.title('요일-시간에 따른 총 대여량')
plt.show()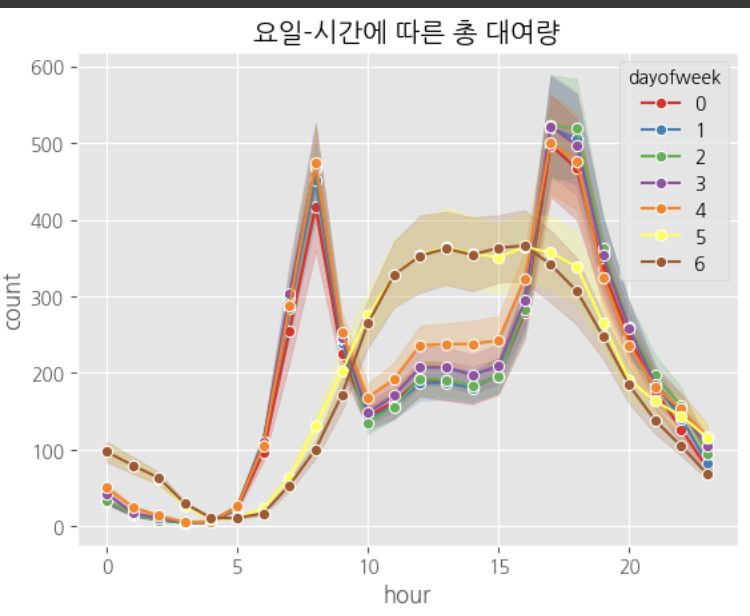
# 예측결과 확인
sns.regplot(data=df, x='temp', y='count', color='gray', line_kws={'color':'red'}, marker='.')
plt.title('기온에 따른 대여량')
plt.show()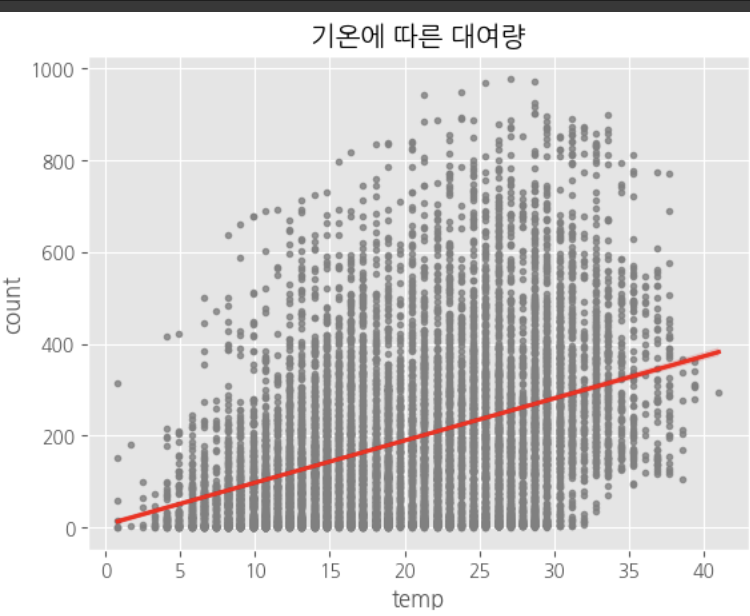
04_와인품종예측_실습
import pandas as pd
import numpy as np
import matplotlib.pyplot as plt
import seaborn as sns
#그래프 스타일
plt.style.use('ggplot')
from sklearn.datasets import load_wine
import pandas as pd
# 데이터셋 로드
wine = load_wine()
# 특징 데이터와 타겟 데이터를 데이터프레임으로 변환
df = pd.DataFrame(data=wine.data, columns=wine.feature_names)
df['target'] = wine.target
# 데이터셋 정보 출력
df.head()
# prompt: Target의 종류 확인
# Target의 종류 확인
df['target'].unique()
# prompt: 데이터 정보 확인
# 데이터 정보 확인
df.info()
# prompt: 데이터의 크기 확인
# 데이터의 크기 확인
df.shape
# prompt: Target을 제외한 나머지 변수들의 분포를 박스플롯으로 확인
import matplotlib.pyplot as plt
# Target을 제외한 나머지 변수들의 분포를 박스플롯으로 확인
plt.figure(figsize=(12, 10))
sns.boxplot(data=df.drop('target', axis=1))
plt.xticks(rotation=45)
plt.show()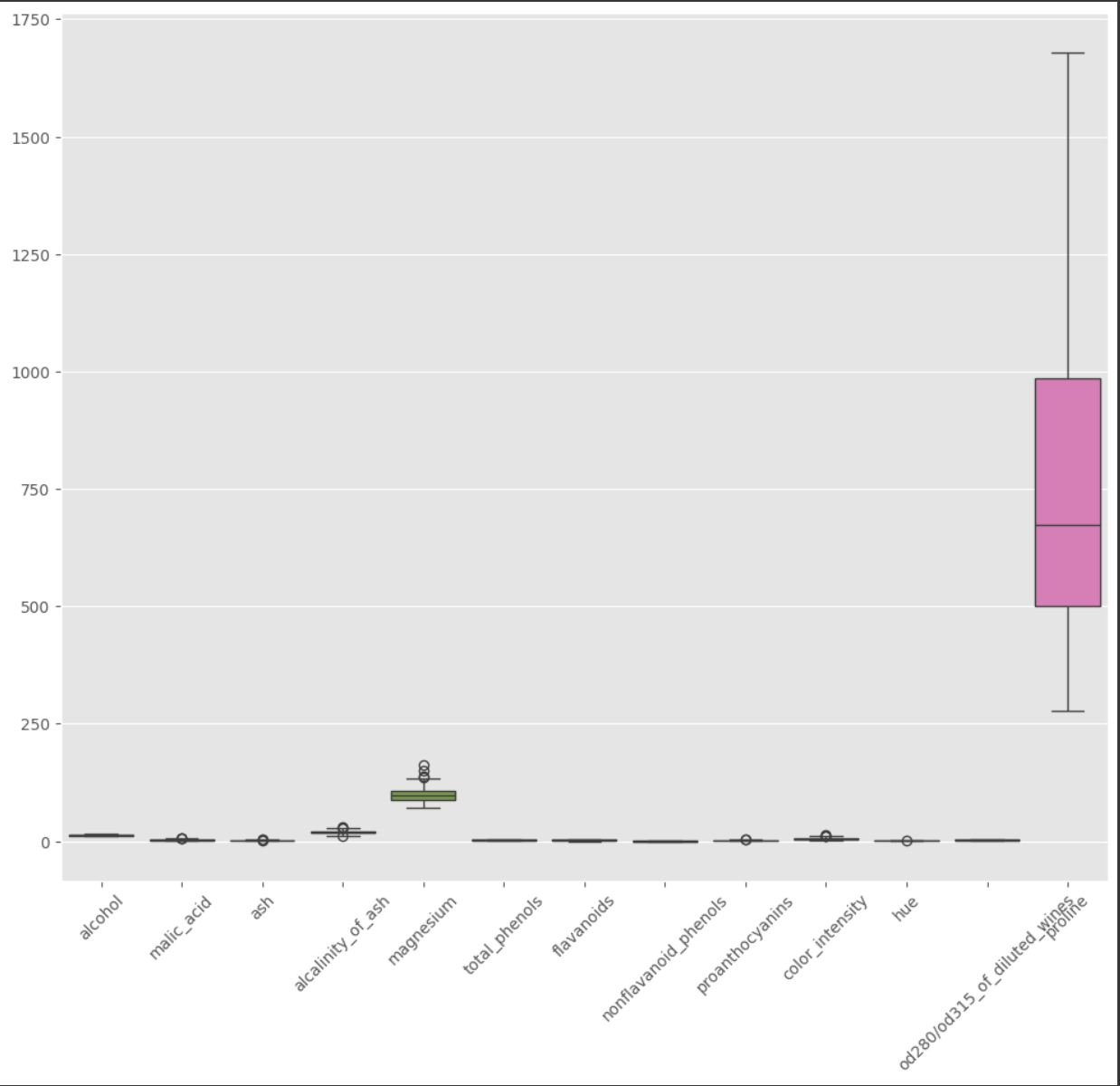
스케일링 하지 않고 학습하기
# prompt: Target을 종속변수로 하고 나머지를 독립변수로 지정
# Target을 종속변수로 하고 나머지를 독립변수로 지정
X = df.drop('target', axis=1)
y = df['target']
# prompt: X, y 데이터 확인
display(X.head())
display(y.head())
# prompt: 훈련데이터화 테스트데이터 분할
from sklearn.model_selection import train_test_split
X_train, X_test, y_train, y_test = train_test_split(X, y, test_size=0.2, random_state=42)
# prompt: Logistic Regression 모델 생성 및 학습하고, 평가 데이터 확인
from sklearn.linear_model import LogisticRegression
from sklearn.metrics import accuracy_score
# 모델 생성 및 학습
model = LogisticRegression()
model.fit(X_train, y_train)
# 예측
y_pred = model.predict(X_test)
# 정확도 평가
accuracy = accuracy_score(y_test, y_pred)
print("Accuracy:", accuracy)Accuracy: 0.9722222222222222
# prompt: DecisionTree 모델 생성 및 학습하고, 평가
from sklearn.tree import DecisionTreeClassifier
# 모델 생성 및 학습
model = DecisionTreeClassifier()
model.fit(X_train, y_train)
# 예측
y_pred = model.predict(X_test)
# 정확도 평가
accuracy = accuracy_score(y_test, y_pred)
print("Accuracy:", accuracy)
#Accuracy: 0.9444444444444444
# prompt: KNN 모델 생성하고 평가
from sklearn.neighbors import KNeighborsClassifier
# 모델 생성 및 학습
model = KNeighborsClassifier()
model.fit(X_train, y_train)
# 예측
y_pred = model.predict(X_test)
# 정확도 평가
accuracy = accuracy_score(y_test, y_pred)
print("Accuracy:", accuracy)
#Accuracy: 0.7222222222222222스케일링하고 학습하기
# prompt: 독립변수 스케일링
from sklearn.preprocessing import StandardScaler
# 스케일링 객체 생성
scaler = StandardScaler()
# 훈련 데이터에 스케일링 적용
X_train_scaled = scaler.fit_transform(X_train)
# 테스트 데이터에 스케일링 적용 (훈련 데이터의 스케일링 정보를 사용)
X_test_scaled = scaler.transform(X_test)
# prompt: 스케일링 된 독립변수의 분포를 박스플롯으로 확인
import pandas as pd
import matplotlib.pyplot as plt
# 스케일링 된 독립변수를 데이터프레임으로 변환
df_scaled = pd.DataFrame(data=X_train_scaled, columns=wine.feature_names)
# 박스플롯으로 분포 확인
plt.figure(figsize=(12, 10))
sns.boxplot(data=df_scaled)
plt.xticks(rotation=45)
plt.show()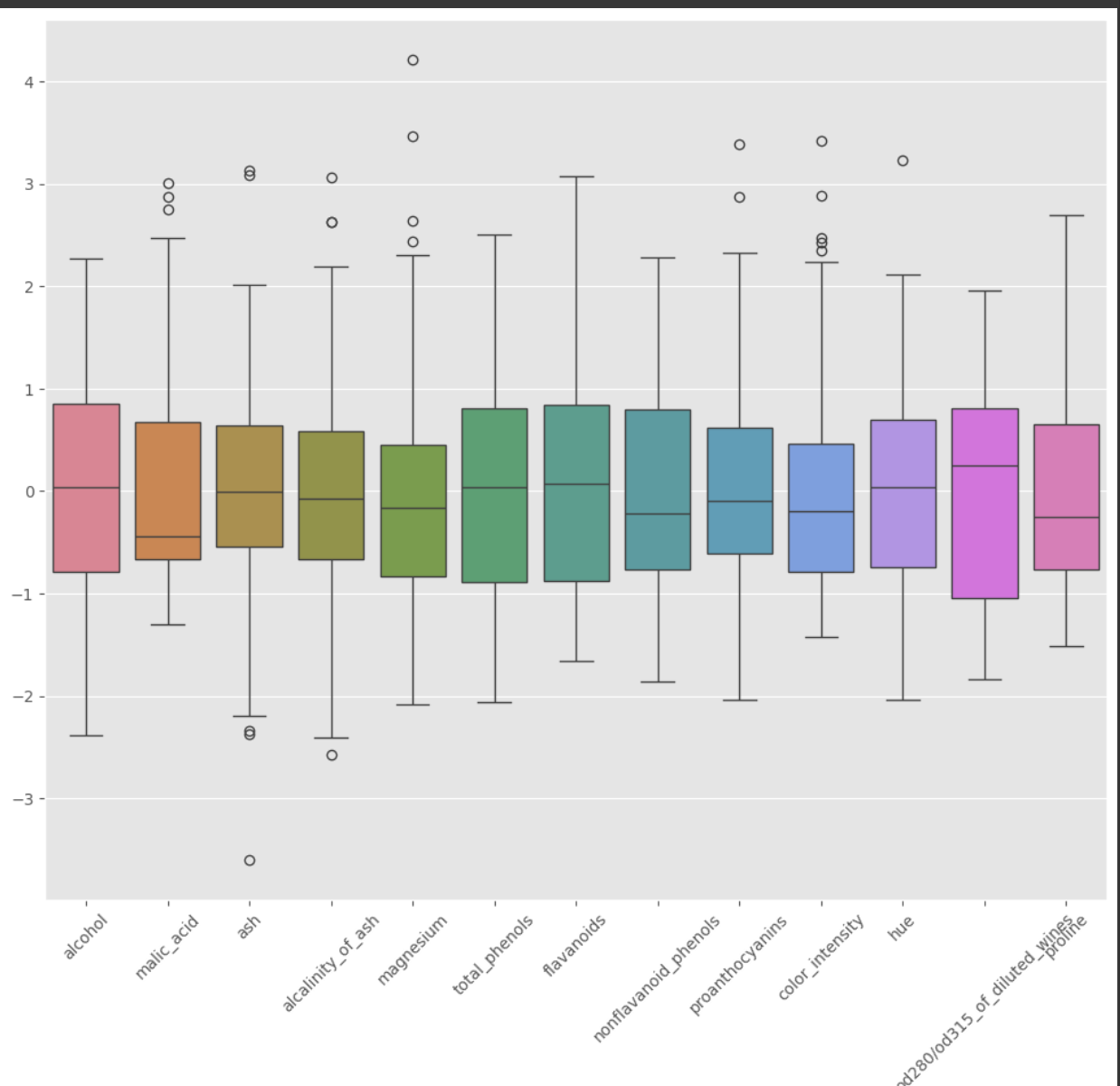
# prompt: # Logistic Regression으로 훈련하고 평가
# 모델 생성 및 학습
model = LogisticRegression()
model.fit(X_train_scaled, y_train)
# 예측
y_pred = model.predict(X_test_scaled)
# 정확도 평가
accuracy = accuracy_score(y_test, y_pred)
print("Accuracy:", accuracy)
#Accuracy: 1.0
# prompt: DecisionTree로 훈련하고 평가
# 모델 생성 및 학습
model = DecisionTreeClassifier()
model.fit(X_train_scaled, y_train)
# 예측
y_pred = model.predict(X_test_scaled)
# 정확도 평가
accuracy = accuracy_score(y_test, y_pred)
print("Accuracy:", accuracy)
#Accuracy: 0.9444444444444444
# prompt: KNN으로 훈련하고 평가
# 모델 생성 및 학습
model = KNeighborsClassifier()
model.fit(X_train_scaled, y_train)
# 예측
y_pred = model.predict(X_test_scaled)
# 정확도 평가
accuracy = accuracy_score(y_test, y_pred)
print("Accuracy:", accuracy)
#Accuracy: 0.9444444444444444# prompt: 예측값 출력하기
# 예측값 출력
print(y_pred)
# prompt: 클래스 별 확률 출력하기
# 모델 예측 확률
y_proba = model.predict_proba(X_test_scaled)
# 클래스별 확률 출력
for i in range(len(y_proba)):
print(f"{i+1}번째 데이터의 클래스별 확률: {y_proba[i]}")
'대외활동 > ai 유니버시티' 카테고리의 다른 글
| [에이블런][AI 스타트업 유니터비시티] 0806 TIL (0) | 2024.08.06 |
|---|---|
| 창업 프로그램 일정 (0) | 2024.07.26 |
| [에이블런] [AI 스타트업 유니버시티] 0722 TIL (1) | 2024.07.22 |
| [에이블런] [AI 스타트업 유니버시티] 0719 TIL (0) | 2024.07.21 |
| [에이블런] [AI 스타트업 유니버시티] 0718 TIL (0) | 2024.07.18 |