2023. 11. 15. 19:54ㆍ데이터분석
[linear Regression's history]
- 선형회귀의 역사는 galton이라는 인물이 아버지의 키로부터 아들의 키를 예측하는 것으로부터 시작되었다.
[vocab]
response (y): = dependent variable, Y-variable, target, outcome
independent variable : = X-variable, feature, attribute
record : row, case, instance, example
intercept : 회귀선의 기울기
regression coefficient : 회귀선의 슬로프(slope=경사)
잔차residuals : 관찰값과 fitted values와 차이 (y - y^)
least squares : 제곱의 잔차 합을 최소화 하는 것(모든 거리가 최소화되는 선을 찾는 것)
[linear regression]
- 지도 학습
- 연속형 변수 ( classification= 이산형)
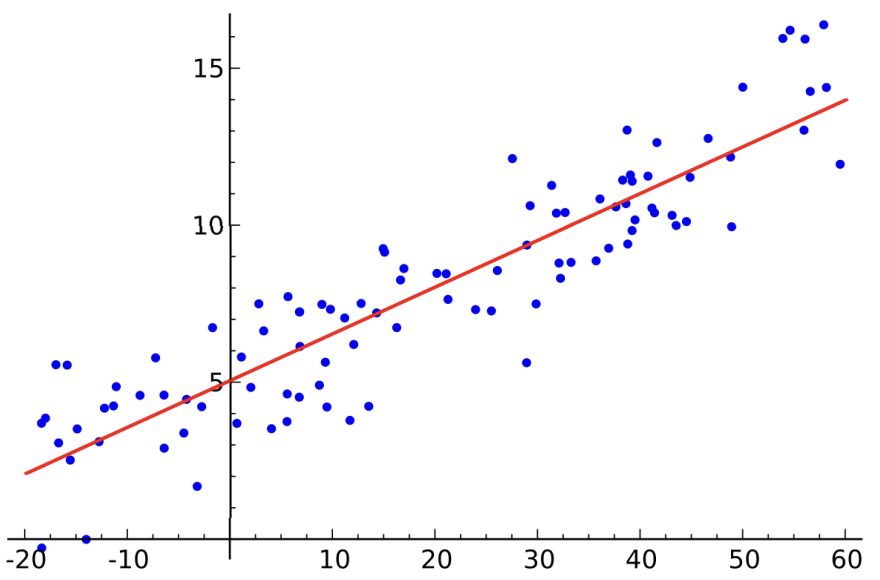
1)단순 선형 회귀(simple linear regression) : x 한개로 타겟 변수를 예측
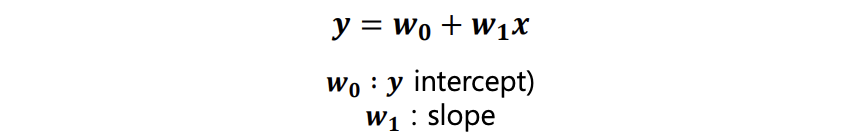
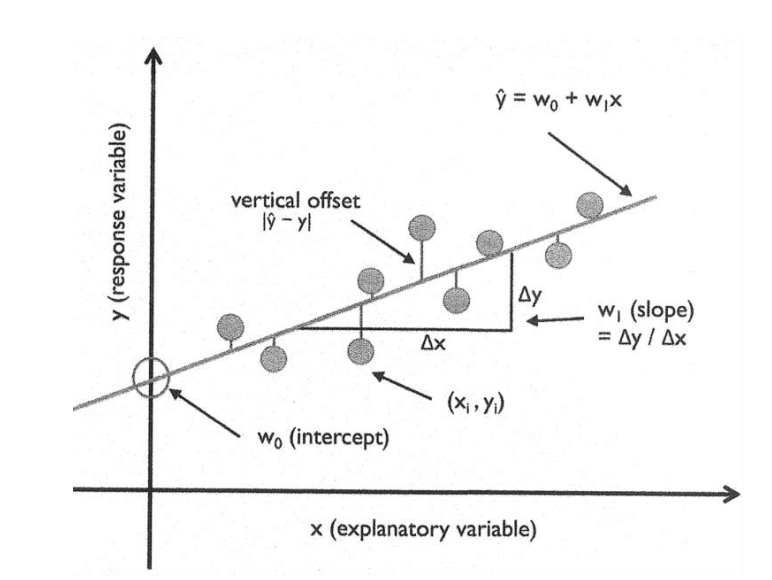
2)다중 선형 회귀(multiple linear regression) : 다수의 x로 y를 예측 하는 것
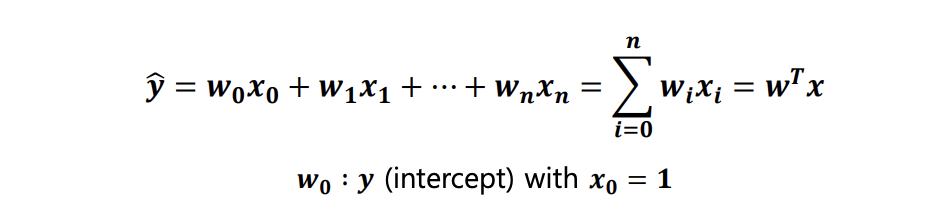
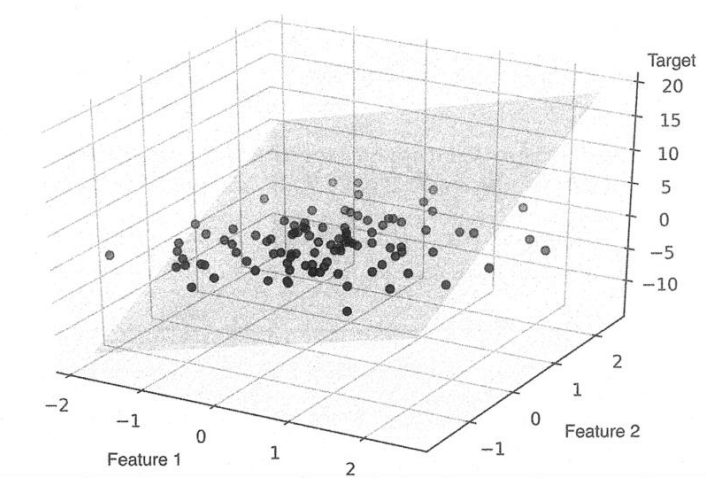
ex) 아들의 키 예측(y) = 아버지의 키 (x1) + 어머니의 키(x2) ...... 어머니 몸무게 ...
[최소제곱법 (least squared method) = 최소자승법 (ordinary least square, OLS)]
목적함수 : 오차의 제곱을 최소화하는 w0, w1을 찾는 것
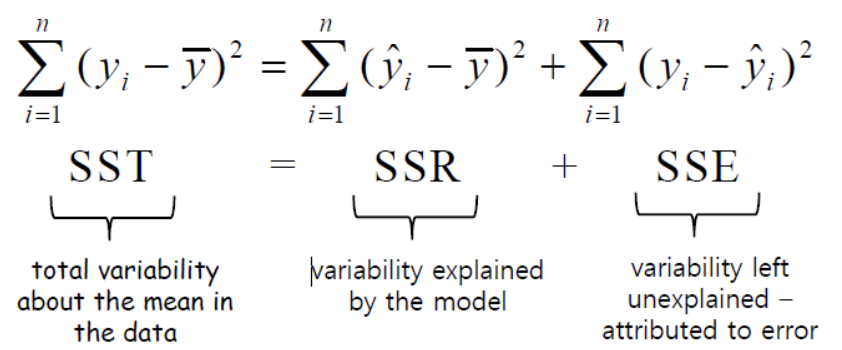
잔차 제곱의 합을 RSS / SSE(sum of squre error)라고함.
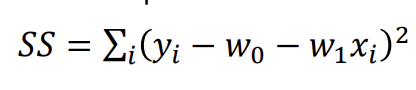
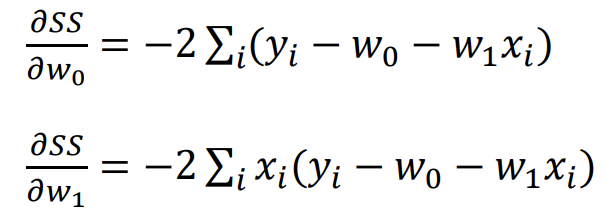
[평가지표(evaluation]
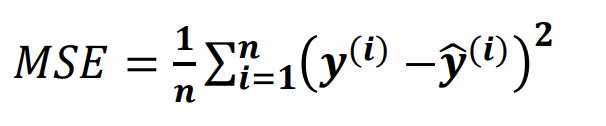
- ss에 n을 나눈 것을 mse라고 한다.
MSE(mean squared errors) : mse는 평균을 모두 합진 것이다. 단점으로는 도메인의 종류에 따라 값이 천차만별이라는 것이다.
예를들어 키 데이터와 손 길이 데이터가 있을 때 키 데이터의 잔차 크기가 더욱 클 것이다.
또 하나더 , 부동산 가격 데이터가 존재한다면 잔차의 크기는 억단위의 크기를 가진 다는 것이다.
이러한 단점을 극복하기 위해 결정계수(coefficient of determination)를 사용한다.
[결정계수(coefficient of determination)] =R^2
- y값 예측을 위해 분산은 불필요
-결정 계수는 0 < R^2 < 1 사이에 존재
- 1에 가까울수록 더 좋은 퍼포먼스를 보인 것
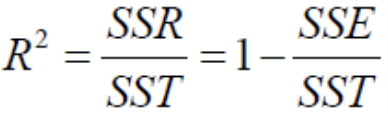
<선형 회귀 코딩 연습>
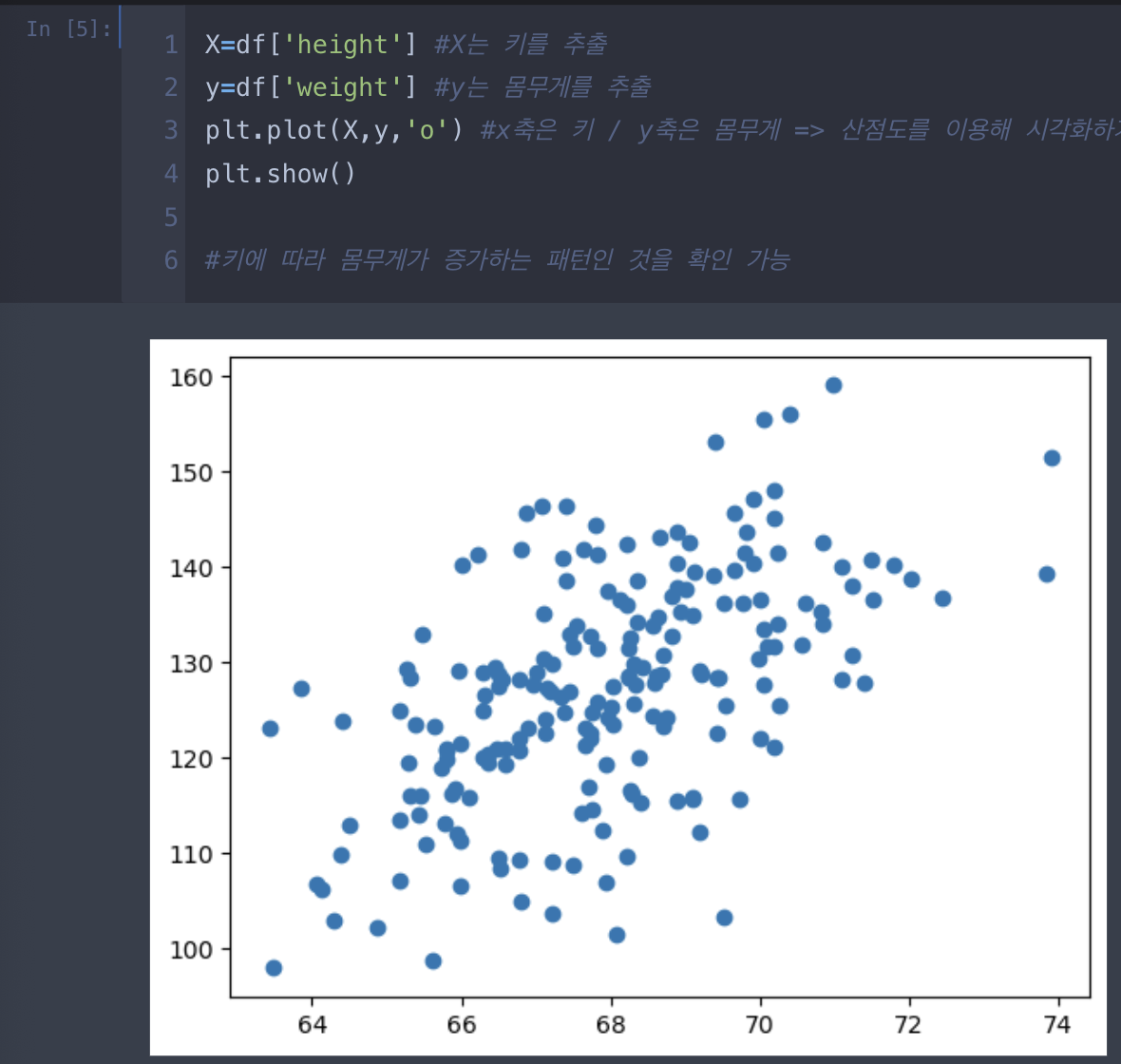
1. 단순 선형 회귀
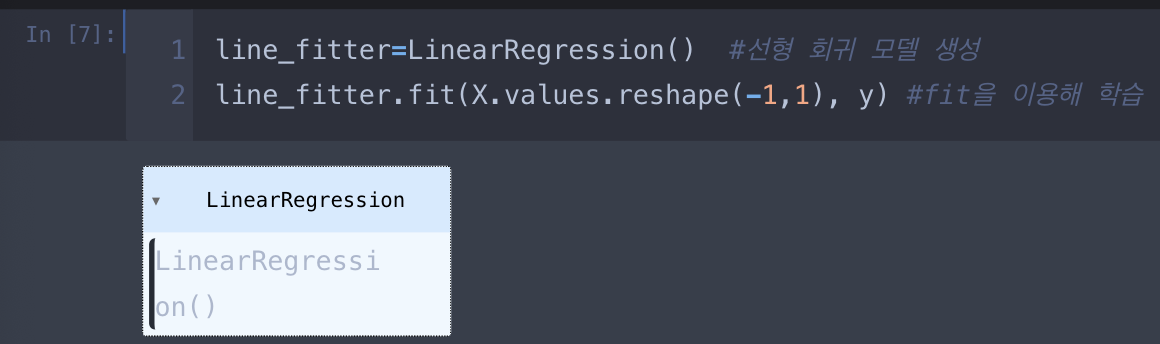
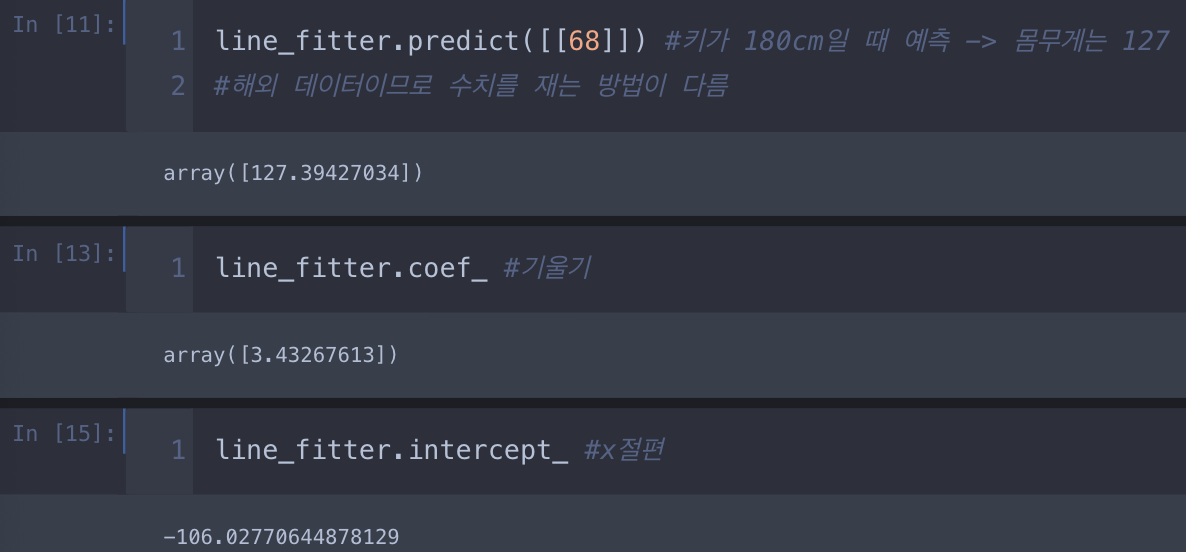
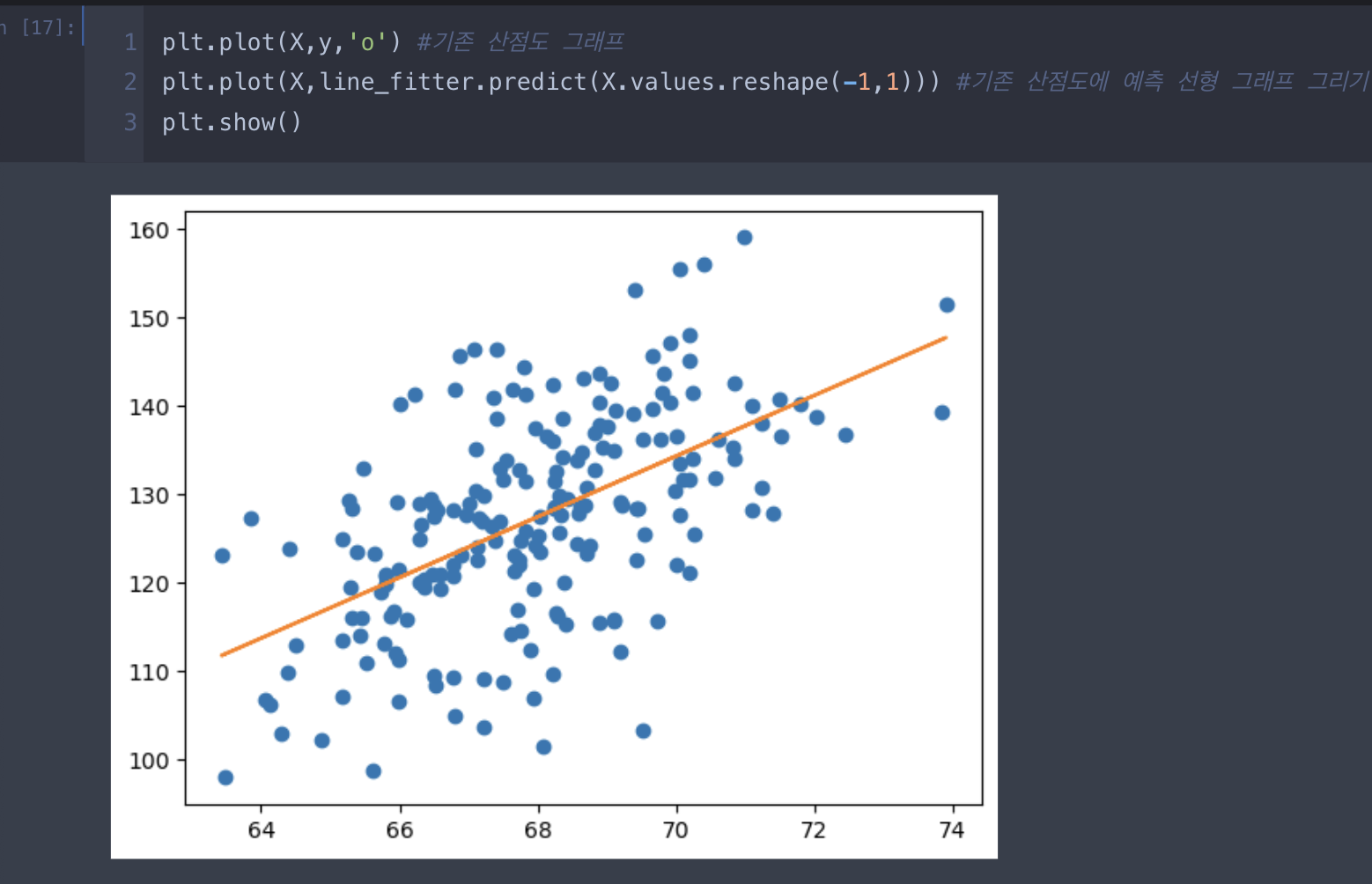
2.다중 선형 회귀
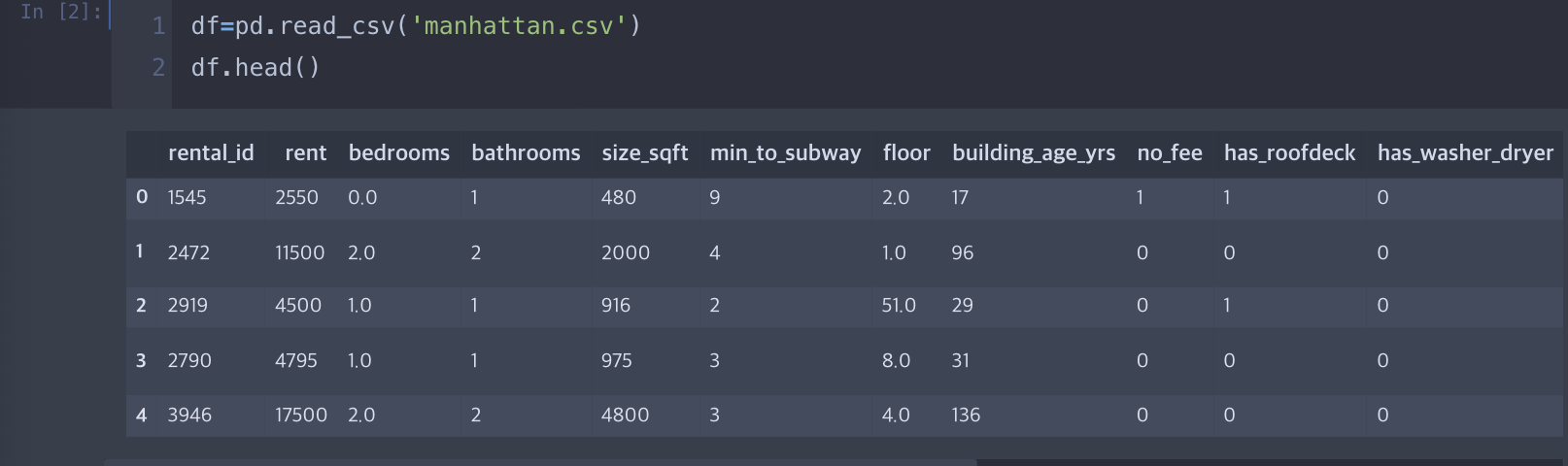
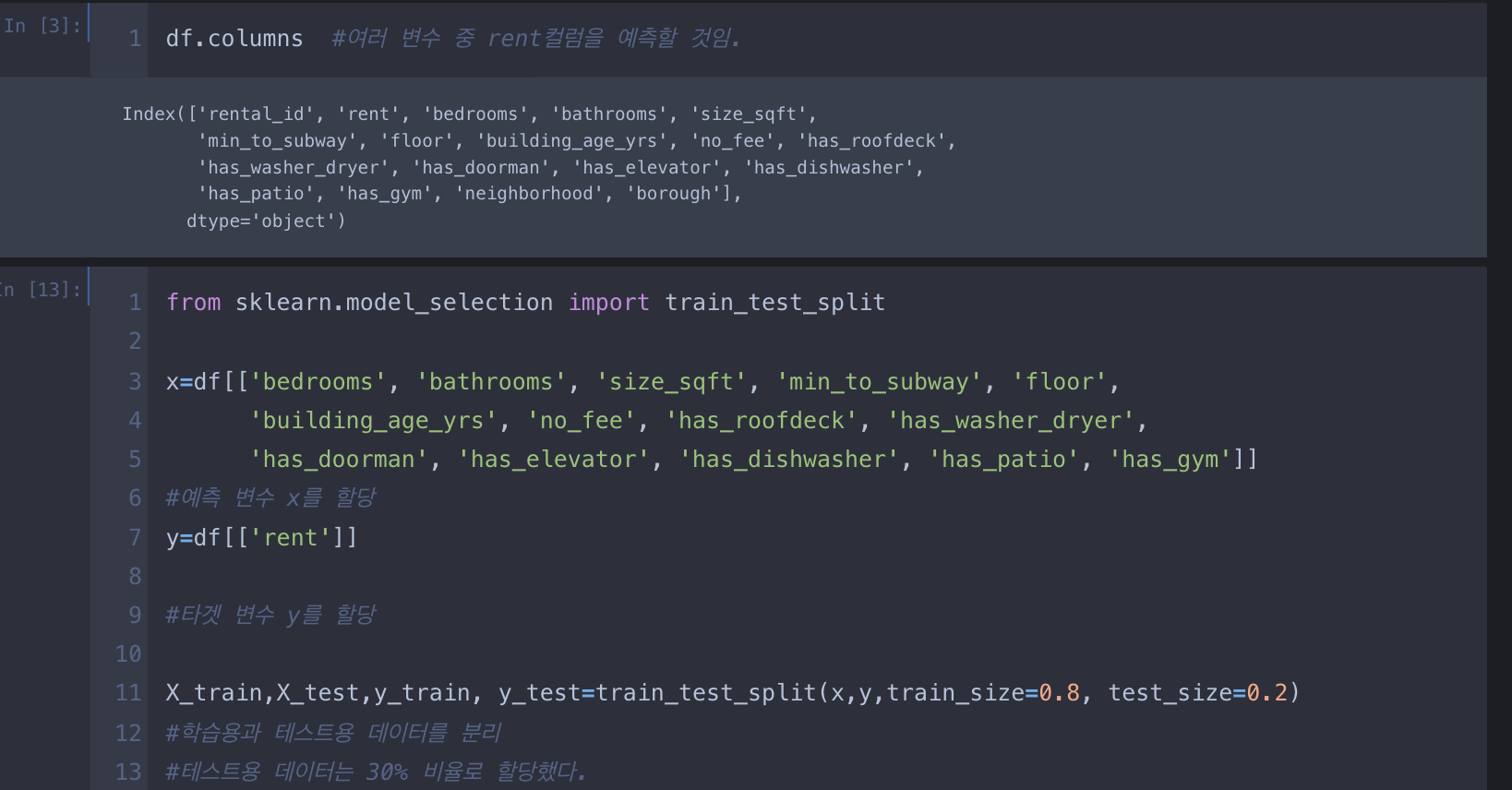

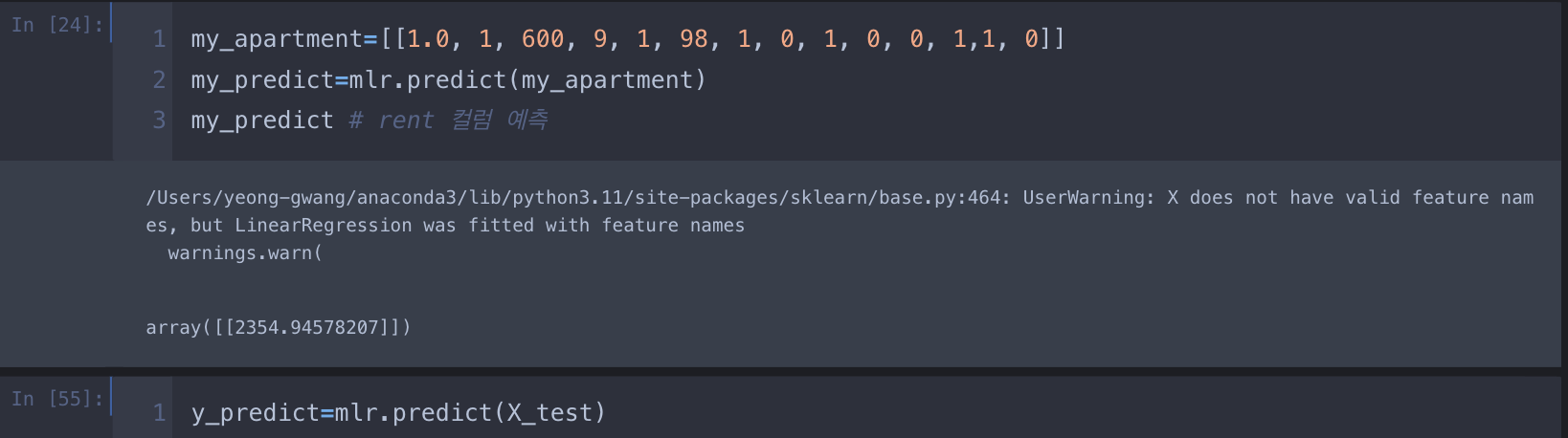
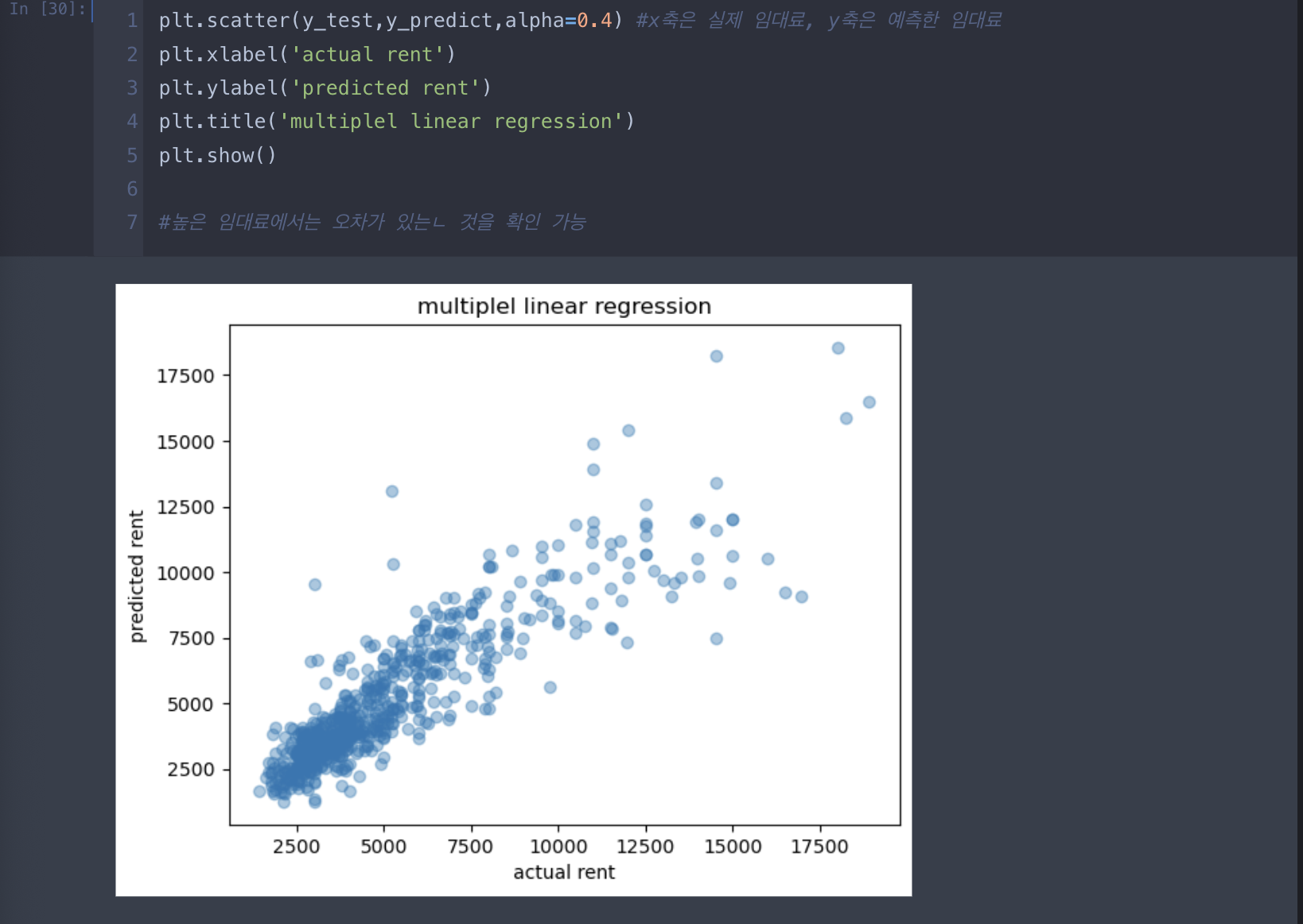
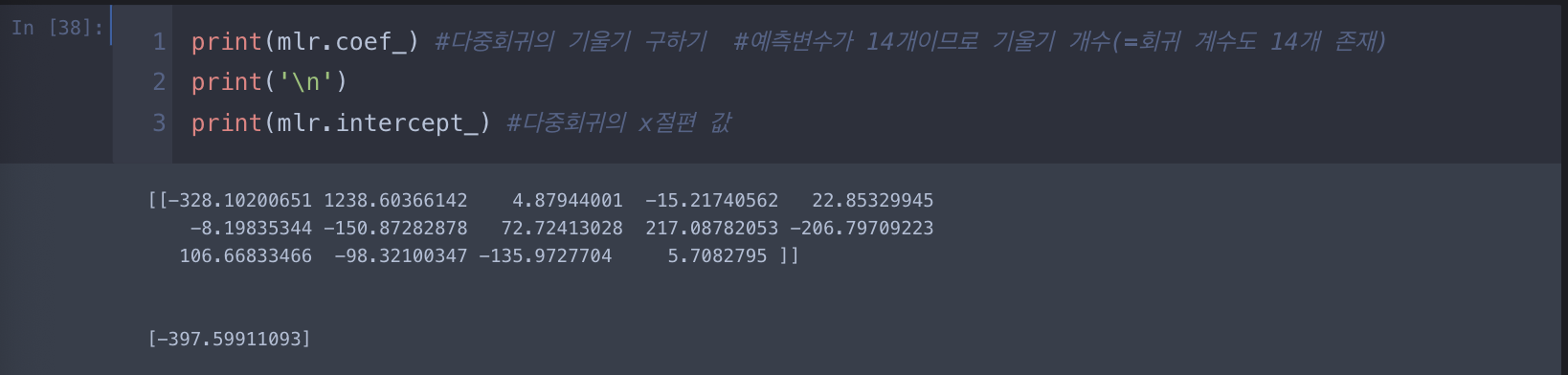

모델의 정확도 평가
- 다중선형회귀 모델의 정확도를 평가할 때는 잔차 분석을 사용(실제 값과 예측 값의 차이를 말함)
- RSS(residual sum of square)는 직선이 미처 y에 대해 설명하지 못한 변화량을 의미
((y-y_predict)**2).sum()
- TSS(total sum of squares)는 y값의 총 변화량을 의미
((y - y.mean()) ** 2).sum()
=> R^2(결정계수)가 클수록 실제값과 예측값이 유사함을 의미하며, 데이터를 잘 설명한다고 이해
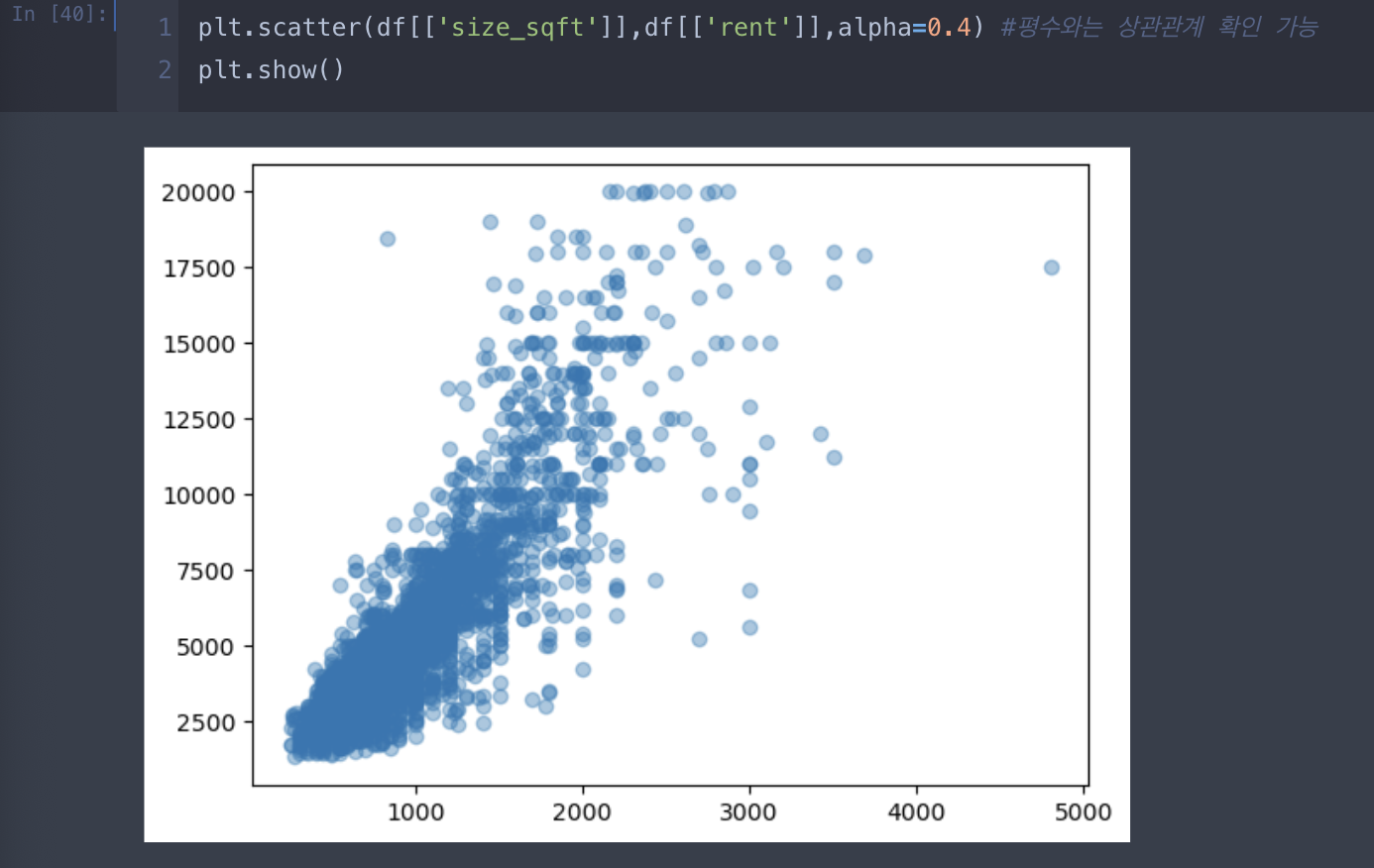
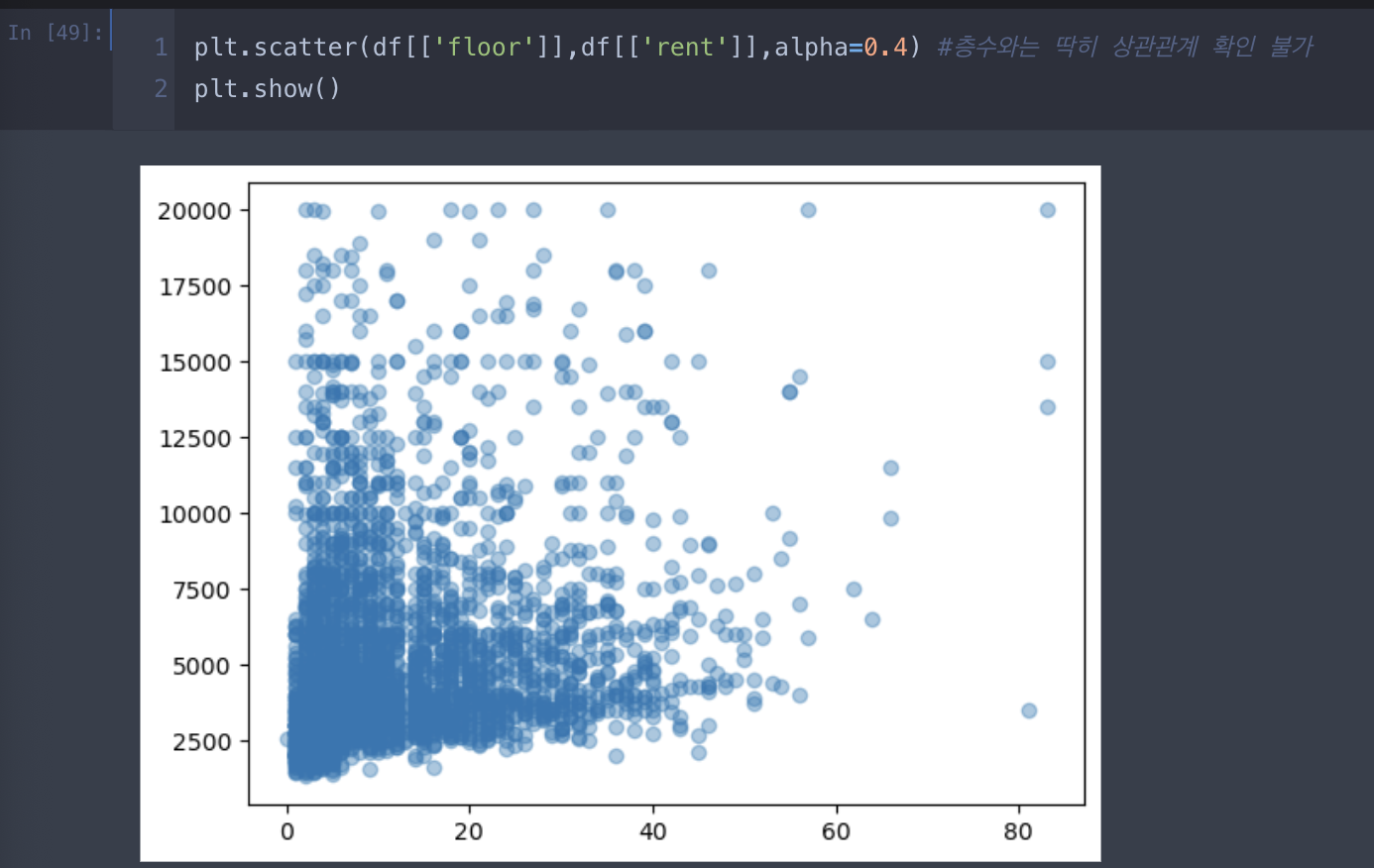
예를 들어, 주택 사이즈와 침실 개수를 기준으로 임대료를 예측하는 모델의 R^2이 0.7인 경우 그 2개의 변수들이 임대료 변동의 70%를 설명한다는 것.
만약 추가로 building_age_yrs를 추가해 R^2이 0.9로 증가했다고 하면 주택 사이즈, 침실 개수, 지어진 연도 이 3개의 변수가 임대료 변수 90%를 설명한다는 것.
<출처>
website
(통계학, 그리고 인공지능(R, python) , 결정계수, 상관계수의 제곱의 차이 증명, 작성자 KIller T Cell, https://rython.tistory.com/17,
결정계수 R^2, 상관계수의 제곱 r^2의 차이 증명(Coefficient of determination VS Squared correlation coefficient)
Introduction 많은 이들이 결정계수 R^2과 상관계수의 제곱 r^2을 동등하게 여긴다. 이는 통계학에서 두드러지는데, 실제로 책 에서는 결정계수를 r^2으로 계산하도록 하고, 통계학 특화 프로그래밍
rython.tistory.com
Medium, 최소제곱법(Least Squared Method), 작성자 조영지(yongji), 2015. 10.21
https://youngji.medium.com/%EC%B5%9C%EC%86%8C%EC%A0%9C%EA%B3%B1%EB%B2%95-least-squared-method-f7357990329f
최소제곱법(Least Squared Method)
최소제곱법은 자료들 사이에서 패턴을 도출해내는데 쓰인다. 아주 직관적이고 간단하기 때문에, 수치해석, 회귀분석 등 다양한 통계학적 접근의 기본이 된다.
youngji.medium.com
아무튼 워라벨, 2019.12.15, https://hleecaster.com/ml-linear-regression-example/
선형회귀(Linear Regression) - 파이썬 코드 예제 - 아무튼 워라밸
본 포스팅에서는 파이썬 라이브러리 scikit-learn을 통해 선형회귀(Linear Regression) 분석을 직접 수행하는 예제를 소개한다. (누구나 쉽게 따라할 수 있는 수준으로 작성했다.)
hleecaster.com
아무튼 워라벨, 2019.12.15, https://hleecaster.com/ml-multiple-linear-regression-example/
다중선형회귀(Multiple Linear Regression) - 파이썬 코드 예제 - 아무튼 워라밸
파이썬 scikit-learn으로 다중선형회귀(Multiple Linear Regression) 분석하는 방법을 코드 예제와 함께 살펴보자.
hleecaster.com
'데이터분석' 카테고리의 다른 글
| linear regression(ridge & lasso) coding implementation (0) | 2023.11.22 |
|---|---|
| numpy,ndarray배열, argsort (0) | 2023.11.16 |
| 데이터사이언스_결측치 처리/인덱싱 (0) | 2023.11.13 |
| 데이터사이언스_원핫인코딩 (0) | 2023.11.13 |
| 데이터 세트 분리 및 시각화(선형 회귀) (0) | 2023.09.17 |