2023. 11. 15. 14:44ㆍ통계학
1. t-test(t 검정)
- t-test는 두 집단의 평균에 통계적으로 유의한 차이가 있는지 알아볼 때 사용하는 통계 분석 기법
- one sample t-test와 two sample t-test가 있음
- t-test를 하기 위해 기본적으로 scipy 패키지로부터 stats라는 모듈을 불러와야 함
< one sample t-test >
- 한 개의 집단을 가지고 t-test를 하는 것
- 한 집단의 평균값이 내가 생각한 값과 다른지 비교할 때 시행하는 것
- stats.ttest_1samp()를 활용

< two sample t-test >
- 두 개의 집단을 가지고 t-test를 하는 것
- 두 집단의 평균 비교를 통해, 두 집단 간의 차이가 통계적으로 유의한지 유의하지 않은지를 확인할 수 있음
- stats.ttest_ind()를 활용

2. Anova 검정
- 세 개 이상의 그룹 간의 평균 차이가 통계적으로 유의미한지를 검정하는 것
- t-검정을 확장해 다수 그룹 간의 차이를 파악할 수 있게 해줌
- 각 그룹의 데이터는 정규 분포를 따르며, 분산이 동일해야 함. 관측치 간에 상호 독립성이 있어야 함
- F 통계량이 크다는 것은 적어도 한 그룹의 평균이 다른 그룹과 다를 가능성이 있다는 것
- 주로 0.05의 유의수준 사용. 유의수준보다 작으면 통계적으로 유의미한 평균 차이가 있다고 할 수 있음

< one way anova >
- 하나의 독립변수에 대해서 세 개 이상의 그룹 간의 평균 차이가 통계적으로 유의미한지 검정
- scipy 패키지에서 stats 모듈을 불러와야 함
- 해당 모듈의 f_oneway() 함수를 사용해 간단하게 F통계량과 유의수준을 확인할 수 있음
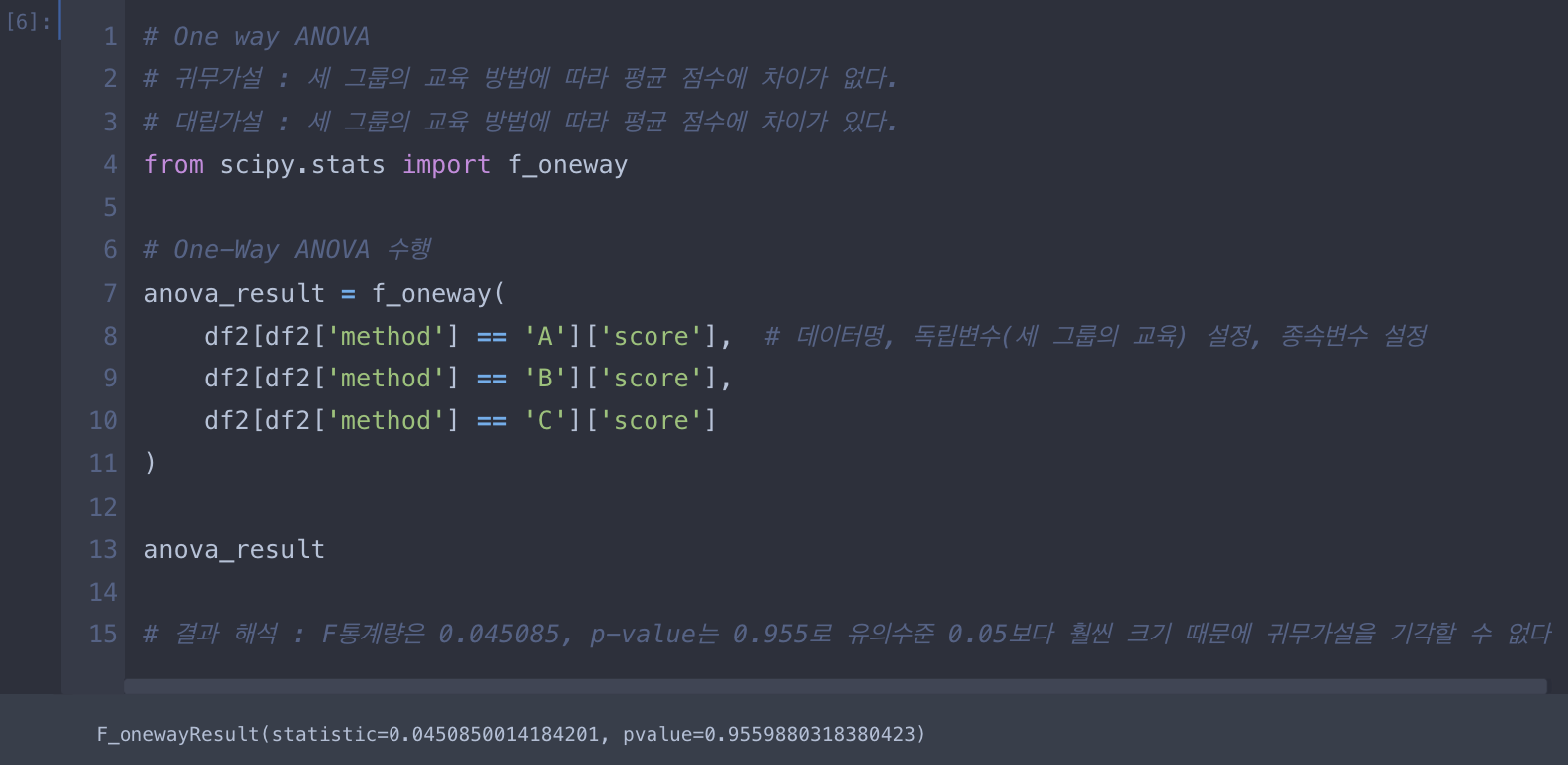
< ANOVA table 만들기 >
1. ols() : Ordinary Least Squares(OLS) 회귀 모델 설정.
- 모델 수식은 종속변수 ~ 독립변수 와 같이 설정
- fit() 메소드를 통해 모델을 데이터에 적합시킴
- 모델의 계수 및 통계 특성 확인
2. anova_lm() : ANOVA 테이블 생성
- model은 ols 함수를 통해 적합시킨 회귀 모델 활용
- typ=2로 설정하여 각 변수에 대해 독립적으로 평가
3. 모델을 만드는 이유
- 주어진 데이터의 종속변수와 독립 변수 간의 관계를 통계적으로 모델링하고 이를 통해 각 변수의 효과 및 상호작용을 평가하기 위함

<상단의 데이터에 대한 결과 해석>
1. method 부분의 F 통계량 : 0.045085
2. method 부분의 유의수준 : 0.955988
- 귀무가설 : 교육 방식에 따라 평균 점수는 차이가 없다.
- 대립가설 : 적어도 한 교육 방식의 평균 점수는 차이가 있다.
- 유의수준 0.05보다 크므로, 귀무가설을 기각할 증거가 부족. 즉, 교육 방식에 따라 평균 점수에 유의한 차이가 있다고 할 수 없음

<사후 분석 표에 대한 해석>
Tukey HSD (Honestly Significant Difference) 다중 비교 방법을 이용해 세 개의 그룹 간에 평균 차이를 비교
1. 평균 차이 (meandiff):
- A 그룹과 B 그룹 간의 평균 차이는 2.2
- A 그룹과 C 그룹 간의 평균 차이는 3.0
- B 그룹과 C 그룹 간의 평균 차이는 0.8
2. 유의미성 (reject):
- 'reject' 열은 각 그룹 간의 평균 차이가 통계적으로 유의미한지 여부를 나타냄
- 모든 경우에서 'False'로 나타나므로, 유의미한 차이가 없다고 할 수 있음
3. p-값 (p-adj):
- 'p-adj' 열은 각 그룹 간의 평균 차이에 대한 수정된 p-값을 나타냄
- 모든 경우에서 p-값이 0.05보다 크므로, 유의미한 차이를 찾을 수 없다고 판단됨
4. 신뢰구간 (lower, upper):
- 'lower'와 'upper'는 각 그룹 간의 평균 차이에 대한 95% 신뢰구간을 나타냄
- 모든 경우에서 신뢰구간이 0을 포함하고 있어, 평균 차이가 0일 가능성이 있음을 나타냄
- 결과적으로, 세 그룹 간에는 통계적으로 유의미한 평균 차이가 없다고 해석할 수 있음. 즉, 모든 경우에서 귀무가설을 기각할 충분한 증거가 나타나지 않음
< two way ANOVA >
- 두 개의 독립 변수가 종속 변수에 미치는 영향을 파악하기 위함
- 주로 F통계량과 p-value를 통해 통해 통계적 유의미함을 확
- 유의미한 결과가 나온다면, 어떤 독립 변수가 종속 변수에 가장 큰 영향을 미치는지, 상호작용이 있는지 등 파악할 수 있음
- Two way ANOVA는 One Way ANOVA처럼 간단한 함수가 있지는 않음. 따라서 모델을 만들고 테이블을 만들어서 확인해야 함
- statsmodels라는 패키지에 있는 모듈들을 활용


<상단의 데이터에 대한 결과 해석>
1. method 부분의 F 통계량 : 2.281043
2. method 부분의 유의수준 : 0.122257
- 귀무가설 : 교육 방식에 따라 평균 점수는 차이가 없다.
- 대립가설 : 적어도 한 교육 방식의 평균 점수는 차이가 있다.
- 유의수준 0.05보다 크므로, 귀무가설을 기각할 증거가 부족. 즉, 교육 방식에 따라 평균 점수에 유의한 차이가 있다고 할 수 없음
3. student 부분의 F 통계량 : 3.535941
4. student 부분의 유의수준 : 0.071300
- 귀무가설 : 학생에 따라 평균 점수는 차이가 없다.
- 대립가설 : 적어도 한 학생의 평균 점수는 차이가 있다.
- 유의수준 0.05보다 크므로, 귀무가설을 기각할 증거가 부족. 즉, 학생에 따라 평균 점수에 유의한 차이가 있다고 할 수 없음.

