2024. 7. 18. 16:02ㆍ데이터분석
[시계열 분석 기본 개념]
1. 정상성과 비정상성
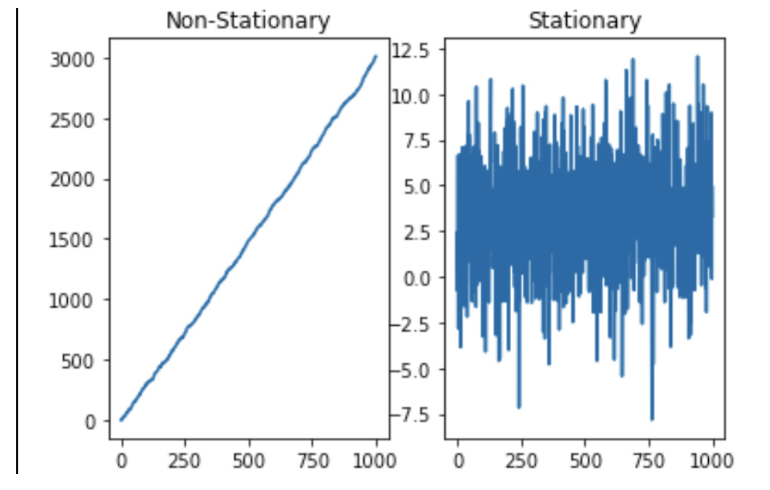
정상성이란 ARIMA 모델링을 통해 시계열 데이터를 분석할 때 필수적으로 고려해야하는 가정으로 시점에 무관하게 과거, 현재, 미래의 분포가 같을 때 정상성을 띈다 말하고 추세를 보이거나 계절성을 보이면 비정상성을 띈다고 말한다.
2. 추세, 계절성, 주기성
추세란 데이터가 장기적으로 위로 올라가는지 내려가는지를 말한다.
계절성은 해마다 어떤 특정한 때나 1주일로 봤을 때 특정 요일에 나타나는 계절성 요인을 말한다.
주기성은 고정된 빈도가 아닌 형태로 증가나 감소하는 모습을 보이는 것이다.
계절성은 1면 마다 같은 변화가 생기는 것이고 주기는 1년보다 길고 다양하며 변동폭이 훨씬 크다.

추세 그래프 : 2,3 / 계절성 그래프 : 1, 3 / 주기성 그래프 : 1
3. 백색잡음, 확률 보행
1) 백색잡음(white noise)
정상성을 띄는 대표적인 예로 평균이 0이고 분산이 유한한 확률분포로부터 자기상관이 없게 무작위로 추출된 시계열 데이터를 말한다. 즉, 시계열 데이터를 전처리한다는 것은 백색잡음으로 얻어내는 것을 의미한다 볼 수 있고, 이러한 백색잡음을 통해 모델에서 시계열 데이터 분석과 예측을 실시할 수 있게 된다.
백색작읍은 2가지 속성을 만족해야하고, 하나라도 만족하지 않으면 모델에 대한 개선여지가 있음을 의미한다.
- 잔차들은 평균이 0인 정규분포이며, 일정한 분산을 가져야 한다.
- 잔차들이 시간의 흐름에 따른 상관성이 없어야 한다.
-> 이러한 상관성을 자기상관성(autocorrelation)이라 부른다.
-> 각 데이터 포인트가 각각 독립성을 지니는 것은 시계열 데이터의 기본적인 가정이기도 하며 이를 i.i.d 라고도 부른다.(individually and independently distributed)
-> 이러한 상관성은 ACF, PACF등과 같은 함수들을 통해 확인해 볼 수 있다.
- 시계열 예측 모델이 실제 현상의 트렌드 및 주기를 잘 반영할 수록 잔차의 변동이 작아지게 되고 이를 바탕으로 모델이 개선되었는지 여부를 파악할 수 있습니다.

2) 확률 보행(random walk)
수학에서 확률보행은 어떤 수학적인 공간(예 : 정수)에서 연속적인 무작위 스텝의 이동경로를 묘사하는 수학적인 객체를 말한다. 예시로 동전 던지기로 점수를 매길 때 앞면이 나오면 +1, 뒷면이 나오면 -1로 하고 그래프를 그려보면 확률보행과정 그래프가 완성이 된다.

시계열 데이터 종류
- 국내총샌상량(GDP), 금융데이터, 날씨 or 강수량 데이터, 소비자 물가 지수, 실업률 등
- 시계열 데이터는 연속 시계열 데이터와 이산 시계열 데이터로 나누어진다.
연속 시계열 데이터 : 연속적으로 생성되는 시계열 자료로서, 관측 값들이 연속적으로 연결된 형태의 자료를 의미한다.

이산 시계열 데이터 : 연속 시계열 데이터는 모든 시점이 연결되어 있기 때문에 분석하기 부담스러워 이산 시계열 데이터를 많이 사용한다. 이산 시계열 데이터란 특정 시점에서 측정한 관측값들의 집합을 말한다.

4. 잔차 진단 (시계열 데이터 모델의 기본가정들)
- 잔차에 대한 진단은 정상성, 정규분포, 자기상관성, 등분산성 총 4가지를 검정하게 되며, 이러한 특성은 시계열 데이터 모델의 기본가정 이기도 하다.
1) 정상성(Stationarity)
- 시간에 관계없이 일정한 상태를 유지하는 것
- 내재적인 패턴의 존재를 의미하는 단위근(Unit Root) 존재여부를 검정한다.
- 대표적으로는 ADF 검정(Augemented Dickey-Fuller Test), KPSS 검정(Kwiatkowski-Phillips-Schmidt-Shin Test)이 있고, 이 둘의 귀무가설을 서로 반대임을 주의해야합니다.
-> ADF 검정의 귀무가설(H 0 ) : 단위근(Unit Root) 존재한다 (비정상)
-> KPSS 검정의 귀무가설(H 0 ) : 단위근(Unit Root)이 없다 (정상)
2) 정규분포(Normal distribution)
- 귀무가설(H 0 ) : 정규분포를 따른다.
- 대립가설(H a ) : 정규분포를 따르지 않는다.
- Shapiro-Wilk test, Kolmogorov-Smirnov test 등 다양한 방법들이 있습니다.
3) 자기상관성(Autocorrelation)
- 귀무가설(H 0 ) : 시간이 지나면 autocorrelation 은 0이다. 자기상관관계가 없다.
- 대립가설(H a ) : 시간이 지나면 autocorrelation 은 0이 아니다. 자기상관관계가 있다.
- Ljung-Box test, Portmanteau test 등 다양한 방법들이 있다.
4) 등분산성(Homoscedasticity)
- 귀무가설(H 0 ) : 시간이 지나면 등분산이다.
- 대립가설(H a ) : 시간이 지나면 등분산이 아니다. 발산하는 분산이다.
- Goldfeld-Quandt test, Breusch-Pagan test 등 다양한 방법들이 있다.
5. 시계열 데이터의 처리
시계열 데이터는 추세변동, 계절변동 등 크고 작은 다양한 변동요인들이 다중적으로 중첩되어 있습니다.
이러한 시계열 데이터의 분석을 수행할 때에는 크게 2가지의 접근법을 이용할 수 있습니다.
요소분해법(Decomposision)
- 내포된 변동요인이 고정적인 패턴을 보이는 경우 -> 가법모형(Additive)
- y t =S t +T t +C t +R t
- 선형적이고, Trend, Seasonal, Cycle이 서로 독립적이라 가정할 수 있는 경우에 이용된다.
승법모형(Multiplicative)
- y t =S t ∗T t ∗C t ∗R t
- 비선형적이고, Trend, Seasonal, Cycle이 서로 영향을 주고받는 경우에 이용됩니다.
평활법(Smooting)
- 다양한 변동요인이 고정적인 패턴을 보이지 않는 경우 -> 이동평균 평활법(MA Smoothing)
- 과거로부터 현재까지의 시계열 자료를 대상으로 일정 기간별 이동평균을 계산하고 이들의 추세를 통해 다음 기간을 예측
지수평균 평활법(Exponential Smooting)
- 모든 시계열 자료를 사용하여 평균을 구하고, 시간의 흐름에 따라서 최근 시계열에 더 많은 가중치를 부여하여 미래의 값을 예측
시계열 데이터 처리 방법들
- 변동폭이 일정하지 않은 경우 : log 변환 추세
- 계절성이 존재하는 경우 : 차분(differencing)
[2]시계열 확률모형(stochastic model)
- 모형 동향에 따른 잔차와 잔차의 분포 (Residual): 분석 모형에서 추정되지 않는 잔차(Residual) 또는 시계열 자료의 잔차 오차(Residual Error Series)는 확률 과정을 통해 나타낼 수 있다.
- 이때 고려되는 모델이 확률모형(Stochastic Model)이다.
- 시계열 분석 모델의 설계 혹은 적합한 경우에 시계열 자료는 백색잡음(White Noise)이 되는 것을 바탕으로 한다.
- 예: xt=yt−y^t∼N(0,σ2)x_t = y_t - \hat{y}_t \sim N(0, \sigma^2)
- 여기서, 잔차는 서로 독립적인 공간에 시계열 분석 모델이 실제 상황을 잘 설명하고 있다고 해석할 수 있음을 의미한다.
- 확률모형의 분석 단계 4가지:
- 모델 식별 (Model Identification):
- ACF, PACF 같은 지표와 ARMA, ARIMA와 같은 프로세스를 이용하여 적합한 모델을 선택한다.
- 모수 추정 (Parameter Estimation):
- 선택한 모델에 따라 모수(계수)를 추정하고 점추정을 거친다.
- 통계적 검정 (Statistical Testing):
- 모델의 적합도에 따른 통계적 상정성과 백색잡음에 대한 검정을 수행한다.
- 예측 (Forecasting):
- 시계열 분석 모델을 통해 미래의 값에 대한 예측을 실시한다.
- 모델 식별 (Model Identification):
2-1. 단일 변량 시계열 모델
AR 모델 (자기회귀 모델, AutoRegressive Model)
- 개념: 과거 자신의 관측값으로부터 미래 값을 예측하는 모델.
- 수식: yt=c+ϕ1yt−1+ϕ2yt−2+...+ϕpyt−p+ϵty_t = c + \phi_1 y_{t-1} + \phi_2 y_{t-2} + ... + \phi_p y_{t-p} + \epsilon_t
- 특징:
- 계수(Φ)가 시계열의 과거 값에 미치는 영향을 나타낸다.
- 잔차(ε)는 화이트 노이즈를 가정한다.
MA 모델 (이동 평균 모델, Moving Average Model)
- 개념: 과거 오차 항을 이용하여 현재의 값을 예측하는 모델.
- 수식: yt=c+θ1ϵt−1+θ2ϵt−2+...+θqϵt−q+ϵty_t = c + \theta_1 \epsilon_{t-1} + \theta_2 \epsilon_{t-2} + ... + \theta_q \epsilon_{t-q} + \epsilon_t
- 특징:
- 계수(θ)는 과거의 예측 오차에 대한 반응을 나타낸다.
ARMA 모델 (자기회귀 이동 평균 모델, AutoRegressive Moving Average Model)
- 개념: AR 모델과 MA 모델의 특성을 결합한 모델.
- 수식: yt=AR(p)+MA(q)y_t = AR(p) + MA(q)
- 특징:
- 과거의 값과 과거의 예측 오차 모두를 사용하여 현재 값을 예측한다.
- ARMA(1,0)은 AR(1)이고, ARMA(0,1)은 MA(1)과 동일하다.
ARIMA 모델 (차분 자기회귀 이동 평균 모델, AutoRegressive Integrated Moving Average Model)
- 개념: 비정상 시계열 데이터에 대해 차분을 통해 정상성을 확보한 뒤 ARMA 모델을 적용하는 모델.
- 수식: ARIMA(p,d,q)에서 d는 차분의 차수를 나타내며, 차분을 통해 데이터를 정상 시계열로 변환한다.
- 특징:
- p와 q는 AR과 MA의 차수를 나타낸다.
- d는 필요한 차분의 차수를 나타내며, 이를 통해 시계열의 비정상성을 제거한다.
- AIC, BIC, ACF, PACF 등을 사용하여 모델의 차수를 선택한다.
ACF (AutoCorrelation Function, 자기상관함수)
- 정의: 시차(lag)에 따라 같은 변수의 다른 시점 간 상호 연관성을 측정하는 함수이다.
- 특징:
- 시차가 커질수록 일반적으로 상관계수는 0에 수렴한다.
- 시계열 데이터의 정상성 여부를 파악하는 데 사용된다.
- 정상 시계열은 상관계수가 빠르게 0으로 수렴하며, 비정상 시계열은 천천히 감소한다.
- MA, ARMA, ARIMA 모델에서 q 값(이동 평균의 차수)을 추정할 때 유용하다. ACF 그래프에서 상관계수가 처음으로 0을 중심으로 하는 신뢰구간 (보통 ±1.96/√n) 안에 들어가는 지점을 q 값으로 설정할 수 있다.
PACF (Partial AutoCorrelation Function, 부분자기상관함수)
- 정의: 시차에 따른 두 시점 간의 순수한 상호 연관성을 측정하는 함수로, 중간 시점의 변수 영향을 제거한 상태에서의 상관관계이다.
- 특징:
- 각 시차에서, 그 시차에 해당하는 두 시점의 상관관계를 측정하되, 그 사이의 모든 다른 시점들의 영향을 배제한다.
- AR, ARMA, ARIMA 모델에서 p 값(자기회귀의 차수)을 추정할 때 사용된다. PACF 그래프에서 상관계수가 처음으로 0을 중심으로 하는 신뢰구간 내로 들어가는 지점을 p 값으로 설정할 수 있다.
- 시계열 데이터가 AR의 특성을 보이는 경우, PACF는 일반적으로 급격히 감소하고 그 후에는 점차적으로 0에 수렴한다.
https://velog.io/@phs5145/%EC%8B%9C%EA%B3%84%EC%97%B4-%EB%8D%B0%EC%9D%B4%ED%84%B0-Time-series
시계열 데이터 Time-series
시계열이란 일정 시간 간격으로 배치된 데이터들의 수열을 말합니다. 즉, 시간의 흐름이 포함되어 있는 데이터라고 볼 수 있겠습니다.위와 같이 계절성, 추세가 있는 시계열이 있고 없는 시계열
velog.io
-------------------------------------------------------------------------------------------------------------------
[캐글 데이터]
https://www.kaggle.com/competitions/store-sales-time-series-forecasting
Store Sales - Time Series Forecasting | Kaggle
www.kaggle.com
프로젝트 목적 : 데이터를 전처리 모델링의 과정을 통하여 데이터의 추세를 파악하고 'sales' 변수의 미래 값을 예측하는 것이 목표이다.
프로젝트 과정 : 라이브러리 및 데이터 불러오기 -> 데이터 전처리(datetime을 통해 날짜 변환, 결측치 처리, 데이터 병합, 이상치 제거, 정규화, 스케일링), 지연 특성과 이동 평균 추가 함수
-------------------------------------------------------------------------------------------------------------------
<지연 특성과 이동 평균 추가 함수를 설정하는 이유>
- 이동 평균을 사용하면 데이터의 노이즈를 줄이고 장기적인 추세를 더 명확하게 파악할 수 있다. 이는 모델이 노이즈에 덜 민감해지도록 하여 더 안정적인 예측을 할 수 있게 한다. (아래에 추가적인 설명)
--------------------------------------------------------------------------------------------------------------------> 학습 데이터와 검증 데이터 분리 -> 모델 리스트 정의 -> 모델 평가 -> 앙상블 모델 -> sarima 모델 적용 -> sarima 모델을 통하여 미래 예측 시각화
import pandas as pd
import numpy as np
from sklearn.preprocessing import LabelEncoder, PowerTransformer, StandardScaler
from sklearn.impute import SimpleImputer
from sklearn.model_selection import train_test_split, TimeSeriesSplit, cross_val_score
from sklearn.metrics import mean_squared_error, mean_absolute_error, r2_score
import matplotlib.pyplot as plt
from statsmodels.tsa.seasonal import seasonal_decompose
from statsmodels.tsa.statespace.sarimax import SARIMAX
from catboost import CatBoostRegressor
from sklearn.ensemble import RandomForestRegressor, GradientBoostingRegressor, VotingRegressor
from sklearn.linear_model import LinearRegression, ElasticNet
from tensorflow.keras.models import Sequential
from tensorflow.keras.layers import LSTM, Dense
# 데이터 로드 함수
def load_data():
train = pd.read_csv('train.csv')
test = pd.read_csv('test.csv')
holidays = pd.read_csv('holidays_events.csv')
oil = pd.read_csv('oil.csv')
stores = pd.read_csv('stores.csv')
transactions = pd.read_csv('transactions.csv')
return train, test, holidays, oil, stores, transactions
# 데이터 로드
train, test, holidays, oil, stores, transactions = load_data()
# 날짜 형식 변환 함수
def convert_dates(df_list):
for df in df_list:
df['date'] = pd.to_datetime(df['date'])
convert_dates([train, test, holidays, oil, transactions])
# 유일하게 oil['dcoilwtico']에 결측치가 존재 -> 평균값으로 결측치를 대체
# 결측값 처리 함수
def handle_missing_values(oil, transactions):
imputer = SimpleImputer(strategy='mean')
oil['dcoilwtico'] = imputer.fit_transform(oil[['dcoilwtico']])
transactions['transactions'] = imputer.fit_transform(transactions[['transactions']])
return oil, transactions
oil, transactions = handle_missing_values(oil, transactions)
# 데이터 병합 및 특성 엔지니어링
def merge_datasets(train, test, stores, transactions, oil, holidays):
le_family = LabelEncoder()
for df in [train, test]:
df['family'] = le_family.fit_transform(df['family'])
df = df.merge(stores, on='store_nbr', how='left')
df = df.merge(transactions, on=['date', 'store_nbr'], how='left')
df = df.merge(oil, on='date', how='left')
df = df.merge(holidays, on='date', how='left')
df.fillna(0, inplace=True)
return train, test
train, test = merge_datasets(train, test, stores, transactions, oil, holidays)
# 특성 엔지니어링 (datetime을 이용하여 날짜 분해)
def feature_engineering(df):
df['day'] = df['date'].dt.day
df['month'] = df['date'].dt.month
df['year'] = df['date'].dt.year
df['dayofweek'] = df['date'].dt.dayofweek
return df
train = feature_engineering(train)
test = feature_engineering(test)=
# 이상치 제거 함수 (Q1 - 1.5 * IQR = 이상치 하한값, Q3 + 1.5 * IQR = 이상치 상한값)
def remove_outliers(df):
Q1 = df['sales'].quantile(0.25)
Q3 = df['sales'].quantile(0.75)
IQR = Q3 - Q1
return df[~((df['sales'] < (Q1 - 1.5 * IQR)) | (df['sales'] > (Q3 + 1.5 * IQR)))]
train = remove_outliers(train)
ㅁ
# 지연 특성과 이동 평균 추가 함수
def add_lag_features(df):
for lag in range(1, 8):
df[f'lag_{lag}'] = df['sales'].shift(lag)
df['rolling_mean_7'] = df['sales'].rolling(window=7).mean()
df['rolling_mean_14'] = df['sales'].rolling(window=14).mean()
return df.dropna()
train = add_lag_features(train)
# 테스트 데이터에 지연 특성과 이동 평균 추가
def add_lag_features_to_test(train, test):
for lag in range(1, 8):
test[f'lag_{lag}'] = train['sales'].shift(lag).values[-len(test):]
test['rolling_mean_7'] = train['sales'].rolling(window=7).mean().values[-len(test):]
test['rolling_mean_14'] = train['sales'].rolling(window=14).mean().values[-len(test):]
test.fillna(0, inplace=True)
return test
test = add_lag_features_to_test(train, test)rolling : 데이터를 윈도우(window) 크기만큼 이동하면서 계산하는 방법
rolling(window=7).mean() : 7의 크기 값의 평균을 계산하고 그 크기만큼 이동
rolling(window=7).mean() : 14의 크기 값의 평균을 계산하고 그 크기만큼 이동
window 크기를 높게 설정하면 어떤 결과가 발생할까? (window 크기를 365로 설정)



좌 : window 크기를 높게 설정, 우 : window 크기를 낮게 설정
=> window 크기를 높게 설정하는 경우 mse값과 결정계수 값이 근소하게 낮아지는 것을 확인하였음.
# 파워 변환 함수
def apply_power_transformer(train):
pt = PowerTransformer()
train['sales'] = pt.fit_transform(train[['sales']])
train['sales'] = np.maximum(train['sales'], 0)
return train
#powertransformer 변환은 데이터를 가우시안 분포로 더 가깝게 만들기 위해 사용한다.
train = apply_power_transformer(train)PowerTransformer() 변환은 데이터를 가우시안 분포로 더 가깝게 만들기 위해 사용함.
# 특성 스케일링
scaler = StandardScaler()
X = train.drop(['id', 'sales', 'date'], axis=1)
y = train['sales']
X_scaled = scaler.fit_transform(X)
X_test = scaler.transform(test.drop(['id', 'date'], axis=1))
# 학습 데이터와 검증 데이터 분리
X_train, X_valid, y_train, y_valid = train_test_split(X_scaled, y, test_size=0.2, random_state=42)
# 데이터 형태 확인
print("Train shape:", X_train.shape)
print("Validation shape:", X_valid.shape)
print("Test shape:", X_test.shape)스케일링 : StandardScaler를 사용하여 진행
종속변수 : sales
독립변수 : id, sales, date를 제외한 변수
[모델 리스트 정의]
LinearRegression
ElasticNet : Lidge Regression과 Lasso Regression의 속성이 포함된 알고리즘
https://ttrhtt12.tistory.com/57
[linear regression]regularization - ridge/lasso
ttrhtt12.tistory.com
RandomForestRegressor
GradientBoostingRegressor
CatBoostRegressor
*데이터의 양이 많아 전체 데이터의 20%만 사용하여 부담을 줄여주었다.
# 데이터 샘플링 (전체 데이터의 20%만 사용)
X_train_sample, _, y_train_sample, _ = train_test_split(X_train, y_train, test_size=0.8, random_state=42)
# 모델 리스트 정의
models = {
"Linear Regression": LinearRegression(),
"ElasticNet": ElasticNet(random_state=42),
"Random Forest": RandomForestRegressor(random_state=42, n_estimators=20, max_depth=5, n_jobs=-1),
"Gradient Boosting": GradientBoostingRegressor(random_state=42, n_estimators=20, max_depth=5),
"CatBoost": CatBoostRegressor(random_state=42, iterations=20, depth=5, silent=True)
}
# 평가 함수 정의
def evaluate_model(name, model, X_train, y_train, X_valid, y_valid):
model.fit(X_train, y_train)
y_pred = model.predict(X_valid)
mse = mean_squared_error(y_valid, y_pred)
mae = mean_absolute_error(y_valid, y_pred)
r2 = r2_score(y_valid, y_pred)
print(f"{name} - MSE: {mse:.4f}, MAE: {mae:.4f}, R^2: {r2:.4f}")
return model
# 모든 모델 평가
best_model = None
best_score = float('inf')
for name, model in models.items():
trained_model = evaluate_model(name, model, X_train_sample, y_train_sample, X_valid, y_valid)
score = mean_squared_error(y_valid, trained_model.predict(X_valid))
if score < best_score:
best_score = score
best_model = trained_model평가 모델은 MSE(Mean Absolute Error), MAE(Mean Squared Error), R2 Score을 사용하였다.
<MSE>
실제 정답 값과 예측 값의 차이를 제곱한 뒤 평균을 구한다.
직관적이지만 제곱을 하기 때문에 1미만의 에러는 작아지고, 그 이상의 에러는 커진다. 또한 실제 정답보다 낮게 예측했는지, 높게 했는지를 파악하기 힘들다.
<MAE>
실제 정답 값과 예측 값의 차이를 절댓값으로 변환한 뒤 합산하여 평균을 구한다.
직관적이지만 실제 정답보다 낮게 예측했는지, 높게 했는지를 파악하기 힘들다.


<R2 SCORE>
실제 값의 분산 대비 예측값의 분산 비율을 의미하며 1에 가까울 수록 좋다.

Linear Regression - MSE: 0.0723, MAE: 0.2204, R^2: 0.7793
ElasticNet - MSE: 0.3278, MAE: 0.5122, R^2: -0.0000
Random Forest - MSE: 0.1607, MAE: 0.2909, R^2: 0.5100
Gradient Boosting - MSE: 0.0996, MAE: 0.2536, R^2: 0.6962
CatBoost - MSE: 0.0560, MAE: 0.1697, R^2: 0.8291
MSE값이 가장 낮고 결정계수가 1에 가까운 CatBoost가 가장 좋은 예측력을 가지는 것으로 확인된다.
[앙상블 모델 정의]
Ensemble이란?
머신러닝/딥러닝에서 앙상블이란 여러 단일 예측(or 분류)모델을 하나로 엮어 더 좋은 성능의 복합 모델을 만드는 기법을 뜻한다.
# 앙상블 모델 정의
ensemble_model = VotingRegressor(estimators=[
('rf', RandomForestRegressor(random_state=42, n_estimators=50, max_depth=10, n_jobs=-1)),
('gb', GradientBoostingRegressor(random_state=42, n_estimators=50, max_depth=10)),
('cat', CatBoostRegressor(random_state=42, iterations=50, depth=10, silent=True))
])
#분류 문제에서는 하드보팅(각 분류기의 예측 결과 중 다수결로 최종 예측 결정) / 소프트보팅(각 분류기의 클래스 확률을 평균내어 최종 예측을 결정,
#가장 높은 확률을 가지는 클래스를 최종 예측으로 선정)방법이 존재하지만, 회귀 문제에서는 이 개념이 적용되지 않음. votingregressor는
#여러 회귀 모델의 예측값을 평균내어 최종 예측값을 도출한다.
# 앙상블 모델 학습 및 평가
ensemble_model.fit(X_train_sample, y_train_sample)
y_pred = ensemble_model.predict(X_valid)
mse = mean_squared_error(y_valid, y_pred)
mae = mean_absolute_error(y_valid, y_pred)
r2 = r2_score(y_valid, y_pred)
print(f"Ensemble Model - MSE: {mse:.4f}, MAE: {mae:.4f}, R^2: {r2:.4f}")본 프로젝트에서 앙상블은 랜덤포레스트, 그래디언트부스트, 캣부스트 알고리즘을 포함한다.
앙상블을 진행 시 분류 문제에서는 하드보팅(각 분류기의 예측 결과 중 다수결로 최종 예측 결정)과 소프트보팅(각 분류기의 클래스 확률을 평균내어 최종 예측을 결정 - 가장 높은 확률을 가지는 클래스를 최종 예측으로 선정)방법이 존재하지만, 회귀 문제에서는 이 개념이 적용되지 않는다.
따라서, votingregressor는 여러 회귀 모델의 예측값을 평균내어 최종 예측값을 도출한다.
[모델링 결과]
Ensemble Model - MSE: 0.0201, MAE: 0.0892, R^2: 0.9388
CatBoost - MSE: 0.0560, MAE: 0.1697, R^2: 0.8291
앙상블 모델과 캣부트스의 결과 값을 비교해보면 CatBoost 알고리즘 보다 Ensemble Model의 값이 더 우수한 것을 확인할 수 있다.
결과
전처리 : 결측치, 이상치 제거, PowerTransformer를 통한 정규화 변환, Scailing, 지연 특성과 이동 평균을 추가(window를 낮게 선정할 시 mse, mae, r^2값이 우수하였음)
전처리 후 모델링을 진행한 결과 다양한 알고리즘 중 Caboost가 가장 우수하였으며, 추가적으로 Ensemble(RandomForest, GradientBoost, CatBoost)을 진행한 결과 mse, mae, r^2 값이 전체적으로 향상된 것을 파악할 수 있었다.
----------------------------------------------------------------------------------------------------------------------
[모델링 추가]
[SARIMA 모델의 기본 개념]
계절성 자기회귀 통합 이동 평균 모델(SARIMA, Seasonal Autoregressive Integrated Moving Average Model)은 복잡한 시계열 데이터, 특히 계절적 변동성을 가진 데이터를 분석하는 데 사용되는 고급 통계적 방법론이다. SARIMA 모델은 ARIMA 모델을 확장하여 계절성 요소를 포함하고 있으며, 계절적 패턴을 보이는 시계열 데이터의 예측에 더욱 적합하게 설계되었다.
[SARIMA 모델의 구성 요소]
1. 자기회귀(AR, Autoregressive) 부분: 이 부분은 시계열 데이터의 현재 값이 과거의 여러 값들에 의존한다는 개념을 나타낸다. 이는 “과거의 정보가 미래를 예측하는 데 도움이 된다”는 아이디어에 근거한다.
2. 차분(Integrated) 부분: 시계열 데이터가 비정상성(non-stationary)을 보일 경우, 일정한 차수의 차분을 통해 데이터를 정상성(stationary)으로 변환한다. 이 과정은 시계열의 추세나 계절성을 제거하는 데 도움이 된다.
3. 이동 평균(MA, Moving Average) 부분: 이 부분은 시계열 데이터의 현재 값이 과거의 예측 오차들에 의존한다는 개념을 나타낸다. 이는 “과거의 오차가 미래 값을 예측하는 데 영향을 준다”는 아이디어에 기반한다.
4. 계절성(Seasonality) 부분: 이 부분은 기본 ARIMA 모델에 계절적 요소를 추가한다. 계절성 차분과 계절성 AR, MA 요소를 포함하여 계절적 변동성을 모델링한다.
[SARIMA 모델의 활용]
경제 및 금융 데이터 분석: 계절성이 뚜렷한 경제 지표나 주식 가격 예측에 사용된다.
기상학: 계절별 기상 변화 예측에 활용된다.
수요 예측: 소매업에서 계절별 판매량 예측에 사용될 수 있다.
# 시계열 데이터 분해 및 시각화
y = train.groupby('date').sum()['sales']
y = y.asfreq('D').fillna(method='ffill')
decomposition = seasonal_decompose(y, model='additive')
#additive(데이터가 추세T, 계절성S, 잔차(R)의 합으로 구성 / multiplicative (데이터가 추세T, 계절성S, 잔차(R)의 곱으로 구성 - 데이터가 비선형적일 때 사용)
fig = decomposition.plot()
plt.show()
# SARIMA 모델 파라미터 설정 및 학습
pdq = [(0, 1, 1), (1, 1, 1), (1, 1, 2), (2, 1, 1)]
seasonal_pdq = [(0, 1, 1, 12), (1, 1, 1, 12), (1, 1, 2, 12), (2, 1, 1, 12)]
param_list = []
param_seasonal_list = []
results_AIC_list = []
for param in pdq:
for param_seasonal in seasonal_pdq:
try:
mod = SARIMAX(y, order=param, seasonal_order=param_seasonal,
enforce_stationarity=False, enforce_invertibility=False)
results = mod.fit()
param_list.append(param)
param_seasonal_list.append(param_seasonal)
results_AIC_list.append(results.aic)
except:
continue
decomposition = seasonal_decompose(y, model = 'additive')
- additive(데이터가 추세T, 계절성S, 잔차(R)의 합으로 구성
- multiplicative (데이터가 추세T, 계절성S, 잔차(R)의 곱으로 구성 - 데이터가 비선형적일 때 사용)
[SARIMA 모델 파라미터 설정 ]
- pdq: 이 리스트는 비계절성(non-seasonal) ARIMA 모델의 파라미터 (p,d,q)(p, d, q)를 정의한다.
- p: AR(자기회귀) 항의 차수
- d: 차분을 통해 데이터의 비정상성을 제거하는 차수
- q: MA(이동 평균) 항의 차수
- seasonal_pdq: 이 리스트는 계절성(seasonal) SARIMA 모델의 파라미터 (P,D,Q,m)(P, D, Q, m)를 정의한다.
- P: 계절적 자기회귀 항의 차수
- D: 계절적 차분의 차수
- Q: 계절적 이동 평균 항의 차수
- m: 계절성 주기 (여기서는 12로 설정되어 있으며, 이는 월별 데이터일 경우 1년을 의미)
seasonal_pdq: 계절성 SARIMA 모델의 네 가지 조합을 설정한다.
- (0, 1, 1, 12): 계절적 AR 차수 0, 계절적 차분 차수 1, 계절적 MA 차수 1, 계절성 주기 12
- (1, 1, 1, 12): 계절적 AR 차수 1, 계절적 차분 차수 1, 계절적 MA 차수 1, 계절성 주기 12
- (1, 1, 2, 12): 계절적 AR 차수 1, 계절적 차분 차수 1, 계절적 MA 차수 2, 계절성 주기 12
- (2, 1, 1, 12): 계절적 AR 차수 2, 계절적 차분 차수 1, 계절적 MA 차수 1, 계절성 주기 12
# 결과 정리 및 최적 모델 설정
ARIMA_list = pd.DataFrame({'Parameter': param_list, 'Seasonal': param_seasonal_list, 'AIC': results_AIC_list})
best_model_order = ARIMA_list.sort_values(by='AIC').iloc[0]['Parameter']
best_model_seasonal_order = ARIMA_list.sort_values(by='AIC').iloc[0]['Seasonal']
mod = SARIMAX(y, order=best_model_order, seasonal_order=best_model_seasonal_order,
enforce_stationarity=False, enforce_invertibility=False)
results = mod.fit()
print(results.summary())
results.plot_diagnostics(figsize=(16, 8))
plt.show()

모델 정보
- 모델: SARIMAX(2, 1, 1)x(2, 1, 1, 12)
- (2, 1, 1): 비계절성 ARIMA 파라미터 (p,d,q)(p, d, q)
- p=2p = 2: 자기회귀 차수
- d=1d = 1: 차분 차수
- q=1q = 1: 이동 평균 차수
- (2, 1, 1, 12): 계절성 SARIMA 파라미터 (P,D,Q,m)(P, D, Q, m)
- P=2P = 2: 계절적 자기회귀 차수
- D=1D = 1: 계절적 차분 차수
- Q=1Q = 1: 계절적 이동 평균 차수
- m=12m = 12: 계절 주기
- (2, 1, 1): 비계절성 ARIMA 파라미터 (p,d,q)(p, d, q)
모델 적합도 지표
- Log Likelihood: -8812.069 (로그 가능도, 높을수록 모델이 데이터에 더 잘 맞음을 의미)
- AIC (Akaike Information Criterion): 17638.137 (낮을수록 모델이 더 적합함을 의미)
- BIC (Bayesian Information Criterion): 17675.993 (낮을수록 모델이 더 적합함을 의미)
- HQIC (Hannan-Quinn Information Criterion): 17652.173 (낮을수록 모델이 더 적합함을 의미)
잔차 분석
- Ljung-Box (L1) (Q): 0.00 (잔차의 자기상관성 검정)
- Prob(Q): 0.00 (p-값, 0.05보다 작아 잔차가 백색 잡음이 아님을 의미)
- > Ljung - Box Test : 일정 기간동안 관측치가 랜덤이고, 독립적인지 여부를 검정
- 귀무 : 데이터가 상관관계를 나타내지 않는다.
- 대립 : 데이터가 상관관계를 나타낸다.
- P.value(귀무가설이 참일 확률) < 0.05 (유의수준) -> 대립가설 참
- Jarque-Bera (JB): 822711.81 (잔차의 정규성 검정)
- Prob(JB): 0.00 (p-값, 0.05보다 작아 잔차가 정규 분포를 따르지 않음을 의미)
-> Jarque Bera Test : 왜도와 첨도가 정규분포와 일치하는지 가설검정
- SARIMAX : 잔차의 분포가 정규분포 인가
- 귀무 가설 : 해당 잔차(residual)는 정규분포와 일치한다.
- 대립 가설 : 해당 잔차(residual)는 정규분포와 일치하지 않는다.
- P.value < 0.05 , 해당 잔차(residual)는 정규분포와 일치하지 않는다.
- Heteroskedasticity (H): 0.97 (잔차의 이분산성 검정)
- Prob(H) (two-sided): 0.76 (p-값, 0.05보다 커서 이분산성이 없음을 의미)
- Skew: -7.24 (잔차의 왜도)
- Kurtosis: 111.46 (잔차의 첨도)

1. 잔차 시계열 플롯 (Standardized residual)
- 위치: 왼쪽 상단
- 설명: 잔차 시계열 플롯은 시간에 따른 잔차의 변동을 보여준다. 잔차가 시간에 따라 랜덤하게 분포되어 있으면 모델이 데이터를 잘 설명하고 있는 것이다.
- 해석: 잔차가 특정 패턴 없이 랜덤하게 분포되어 있는지 확인한다. 특정 패턴이나 추세가 있다면 모델이 데이터의 일부 구조를 잘 설명하지 못하고 있을 가능성이 있다.
- 대부분의 잔차가 0을 중심으로 분포하고 있으며, -5에서 5 사이에 주로 위치합니다.
- 몇몇 잔차가 -15와 같은 극단적인 값을 가지며, 이는 이상치 또는 특이값일 수 있습니다.
- 전반적으로 잔차가 랜덤하게 분포하고 있지만, 극단적인 값이 다수 존재하여 모델의 성능에 영향을 미칠 수 있습니다.
2. 히스토그램 및 밀도 추정 (Histogram plus estimated density)
- 위치: 오른쪽 상단
- 설명: 히스토그램은 잔차의 분포를 시각화하고, 커널 밀도 추정(KDE) 곡선과 정규분포 곡선을 겹쳐서 보여준다.
- 해석: 잔차의 분포가 정규분포와 얼마나 일치하는지 확인한다. 정규분포를 따르면 모델이 잘 맞춰진 것이다. 히스토그램이 대칭적이고 정규분포 곡선과 잘 맞아떨어지면 모델이 적절히 잘 맞춰졌다고 볼 수 있다.
- 히스토그램은 잔차가 대체로 정규 분포에 가깝게 분포하고 있음을 보여줍니다.
- 초록색 곡선은 정규 분포를 나타내며, 주황색 곡선은 KDE로 추정된 밀도입니다.
- KDE와 정규 분포 곡선이 대체로 일치하지만, 잔차의 분포가 정규 분포보다 약간 뾰족하거나 꼬리가 두꺼울 수 있음을 시사합니다.
3. Q-Q 플롯 (Normal Q-Q plot)
- 위치: 왼쪽 하단
- 설명: Q-Q 플롯은 잔차가 정규분포를 따르는지 확인하기 위한 도구이다. 이론적 분위수와 실제 잔차의 분위수를 비교하여 플롯한다.
- 해석: 점들이 대각선에 가깝게 분포할수록 잔차가 정규분포를 따른다. 점들이 대각선을 따라 잘 정렬되어 있다면 모델의 잔차가 정규성을 만족한다고 할 수 있다.
- 대부분의 점들이 대각선에 가깝게 분포하여 잔차가 대체로 정규 분포를 따르고 있음을 나타냅니다.
- 그러나 극단적인 점들이 대각선에서 벗어나 있으며, 이는 잔차에 극단값(이상치)이 존재함을 나타냅니다.
4. 자기상관도 (Correlogram)
- 위치: 오른쪽 하단
- 설명: 자기상관도는 잔차의 시차(lag)에 따른 자기상관 계수를 보여준다. 각 점은 특정 시차에서의 자기상관을 나타내며, 신뢰구간을 함께 표시한다.
- 해석: 잔차가 백색잡음(white noise)이라면 대부분의 자기상관 계수는 0에 가깝고, 신뢰구간 내에 있어야 한다. 시차(lag)에서의 자기상관 계수가 신뢰구간을 벗어나지 않으면 잔차가 독립적이고 모델이 적절히 적합되었다고 할 수 있다.
- 대부분의 자기상관 계수(lag 1 이후)가 0에 가깝고 유의미하지 않음을 나타내며, 이는 잔차가 백색 잡음임을 시사합니다.
- 그러나 lag 1에서 유의미한 상관관계가 존재하며, 이는 일부 시차에서 잔차가 상관관계를 가질 수 있음을 나타냅니다.
* 백색잡음과정(White Noise Process)이란 서로 독립이고 동일한 분포를 따르는(independently and identically distributed; i.i.d) 확률변수들의 계열로 구성된 확률과정으로서,
ε_t들이 서로 독립이고 평균 0, 분산 σ^2 을 갖는 확률변수라고 할 때 ε ~ WN(0, σ^2) 라고 표기할 수 있다.
교재에 따라서는 오차항들이 서로 독립이라는 i.i.d 가정 대신에 서로 상관관계가 없다는 비교적 약한 가정을 이용하여 백색잡음과정을 정의한다.

평균과 분산이 일정함을 알 수 있고, 어떠한 추세도 관측되지 않죠.
대표적인 정상 시계열이라고 할 수 있습니다.
https://datalabbit.tistory.com/109
[시계열분석] 백색잡음과정(White Noise Process)
Review 참고 포스팅 : 2021.07.04 - [Statistics/Time Series Analysis] - [시계열분석] 정상성(Stationarity) [시계열분석] 정상성(Stationarity) Review 참고 포스팅 : 2021.02.02 - [Statistics/Time Series Analysis] - [시계열분석] 확
datalabbit.tistory.com
# 미래 예측 및 시각화
forecast_steps = 365
pred_uc = results.get_forecast(steps=forecast_steps)
pred_ci = pred_uc.conf_int()
ax = y.plot(label='Observed', figsize=(14, 7))
pred_uc.predicted_mean.plot(ax=ax, label='Forecast', linestyle='--', color='r')
ax.fill_between(pred_ci.index, pred_ci.iloc[:, 0], pred_ci.iloc[:, 1], color='k', alpha=.25)
plt.title('Long-term Forecast')
plt.xlabel('Date')
plt.ylabel('Sales')
plt.legend()
plt.show()
[미래 예측 시각화]

-----------------------------------------------------------------------------------------------------------
<시계열 실습++>
04) FinanceDataReader
FinanceDataReader는 한국 주식 가격, 미국 주식 가격, 지수, 환율, 암호 화폐 가격, 종목 리스트 등을 제공하는 API 패키지입니다. 우선 해당 패키지를 설치해줍…
wikidocs.net
FinanceDataReader
FinanceDataReader는 한국 주식 가격, 미국 주식 가격, 지수, 환율, 암호 화폐 가격, 종목 리스트 등을 제공하는 API 패키지이다.
프로젝트 목적 : Moving Average, Difference(차분) , Stationary(정상성), Trend(추세), ACF, PCAF, ARIMA, SARIMA에 대하여 추가적으로 조사하고 코드로 구현해본다.
import pandas as pd
import FinanceDataReader as fdr
import matplotlib.pyplot as plt
import numpy as np
krx_stocks = fdr.StockListing('KRX')
krx_stocksStockListing('KRX')를 입력 후 한국 주식 가격 데이터를 불러온다.

start_date = '20210101'
end_date = '20211231'
sample_code = '005930' # 삼성전자
stock = fdr.DataReader(sample_code, start = start_date, end = end_date)
stock
[이동평균 확인]
시계열 데이터를 분석하는 과정에서 시간 흐름에 따라 변동이 크거나 일정하지 않을 경우 비정상성을 지니게 되고 이를 전처리 없이 머신러닝 알고리즘에 학습할 경우 단순 후행 예측, 성능 저하, 잘못된 추론 등의 문제를 야기시킬 수 있다.
단순 이동평균(Simple Moving Average)
1. 개념
- 주어진 기간 동안의 데이터 값의 평균을 계산하여 이동 평균선을 생성한다.
- 예를 들어, 주가 데이터가 있을 때, 5일 이동평균을 계산하면 가장 최근 5일 동안의 주가 평균을 구하게 된다.
2. 계산 방법
- 주어진 데이터 : 주가 데이터
- 윈도우 : 평균을 계산할 기간 (ex : window = 5)
- 계산 : 각 데이터 포인트에서 이전 window 기간 동안의 주가 평균을 계산
3. 장점
- 단순함, 추세 파악 용이
4. 단점
- 지연 : 이동평균은 과거 데이터를 기반으로 하여 계산되므로, 최신 데이터의 변화에 대한 반응이 느림
- 노이즈 필터링 부족 : 단순 이동평균은 모든 데이터 포인트를 동일한 가중치로 평균내기 때문에, 데이터의 노이즈를 충분이 제거하지 못할 수 있음
def SMA(df, col, window=2):
return df[col].rolling(window=window, min_periods=1).mean()
stock['MA(5)'] = SMA(stock, 'Close', 5)
plt.figure(figsize=(10, 6))
plt.plot(stock['Close'], label='Raw')
plt.plot(stock['MA(5)'], label='MA(5)', linestyle='--')
plt.title('Stock Price with 5-Day Moving Average')
plt.xlabel('Date')
plt.ylabel('Price')
plt.legend()
plt.show()

[Exponential Moving Average(EMA)]
1. 개념
- EMA는 과거의 데이터 포인트에 지수적으로 감소하는 가중치를 부여하여 평균을 계산한다. 이는 최신 데이터 포인트에 더 많은 가중치를 두고, 과거 데이터 포인트에 덜 가중치를 주어 최신 변화에 더 민감하게 반응한다.
2. 계산 방법
- EMAt = α⋅Yt + (1−α)⋅EMAt−1

3. 장점
- 빠른 반응 : 최신 데이터에 더 많은 가중치를 부여하여 변화에 빠르게 반응한다.
- 추세 파악 : 단순 이동평균보다 데이터의 추세를 더 정확하게 반영할 수 있다.
4. 단점
- 복잡성 : 단순 이동평균에 비해 계산이 더 복잡합니다.
- 과거 데이터 의존 : 모든 과거 데이터를 사용하므로, 과거 데이터가 많은 경우 계산이 느려질 수 있습니다.
def EMA(df, col, span=2):
return df[col].ewm(span=span).mean()
stock['EMA(5)'] = EMA(stock, 'Close', 5)
plt.figure(figsize=(10, 6))
plt.plot(stock['Close'], label='Raw Data')
plt.plot(stock['EMA(5)'], label='EMA(5)', linestyle='--')
plt.title('Stock Price with 5-Day Exponential Moving Average')
plt.xlabel('Date')
plt.ylabel('Price')
plt.legend()
plt.show()
[푸리에 변환(Fourier Transform)]
1. 개념
- 시간 도메인 : 신호가 시간에 따라 어떻게 변하는지를 나타낸다.
- 주파수 도메인 : 신호가 다양한 주파수 성분으로 어떻게 구성되어 있는지를 나타낸다.
- 푸리에 변환은 시간 도메인의 신호를 주파수 도메인으로 변환하여 각 주파수 성분의 크기와 위상을 계산한다.
2. 푸리에 변환의 주요 특징
- 주파수 성분 분석: 신호가 어떤 주파수 성분으로 이루어져 있는지를 분석할 수 있다.
- 잡음 제거: 주파수 도메인에서 특정 주파수를 제거하여 잡음을 줄일 수 있다.
- 압축: 신호의 주요 주파수 성분만을 사용하여 신호를 압축할 수 있다.
def FFT(df, col, topn=2):
fft = np.fft.fft(df[col])
fft[topn:-topn] = 0
ifft = np.fft.ifft(fft)
return ifft
stock['FFT(30)'] = FFT(stock, 'Close', 30)
plt.figure(figsize=(10, 6))
plt.plot(stock['Close'], label='Raw Data')
plt.plot(stock['FFT(30)'], label='FFT(30)', linestyle='--')
plt.title('Stock Price with Fourier Transform')
plt.xlabel('Date')
plt.ylabel('Price')
plt.legend()
plt.show()
단순 이동평균(Simple Moving Average), 지수 이동평균(Exponential Moving Average), 푸리에 변환(Fourier Transform)을 시각화 한 결과 푸리에 변환이 Raw Data와 유사한 값을 나타낸 것을 확인할 수 있다.
[Modeling]
stock['FFT(30)'] = FFT(stock, 'Close', 30)
# 푸리에 변환 결과에서 실수부와 허수부 분리
stock['FFT(30)_real'] = stock['FFT(30)'].apply(lambda x: x.real)
stock['FFT(30)_imag'] = stock['FFT(30)'].apply(lambda x: x.imag)
# 데이터 분할
X = stock[['Close', 'FFT(30)_real', 'FFT(30)_imag']].iloc[:-1]
y = stock['Close'].shift(-1).dropna()
X_train, X_test, y_train, y_test = train_test_split(X, y, test_size=0.2, random_state=42)
# 모델 훈련
model = LinearRegression()
model.fit(X_train, y_train)
# 예측
y_pred = model.predict(X_test)
y_pred
# 성능 평가
mae = mean_absolute_error(y_test, y_pred)
print(f'MAE: {mae}')
MAE: 693.2582547143872
# 예측 결과 시각화
plt.figure(figsize=(12, 6))
plt.plot(stock.index[-len(y_test):], y_test, label='Actual', color='blue')
plt.plot(stock.index[-len(y_test):], y_pred, label='Predicted', color='orange', linestyle='--')
plt.title('Stock Price Prediction')
plt.xlabel('Date')
plt.ylabel('Price')
plt.legend()
plt.show()

단순 이동평균, 지수 이동평균, 푸리에 변환을 통하여 예측 선을 그려보았다. 단순 이동평균보다 지수 이동평균이 실제 값과 비슷하였고, 푸리에 변환(Fourier Transform)이 그중 가장 비슷한 결과가 나타났다.
이를 바탕으로 푸리에 변환을 이용하여 모델링을 진행하였다.
----------------------------------------------------------------------------------------------------------------------
*시계열 실습+++
(차분에 대하여 더 알아보기)
import numpy as np
import pandas as pd
import matplotlib.pyplot as plt
from statsmodels.tsa.arima.model import ARIMA
from statsmodels.graphics.tsaplots import plot_acf, plot_pacf
# 데이터 생성 (예제 데이터 사용)
np.random.seed(0)
date_range = pd.date_range(start='20210101', periods=100, freq='D')
data = np.random.randn(100).cumsum() # 누적합을 사용하여 트렌드가 있는 데이터 생성
stock = pd.DataFrame(data, index=date_range, columns=['Close'])
stock

# 1차 차분을 통한 데이터 안정화
stock['Close_diff1'] = stock['Close'].diff()
# 2차 차분을 통한 데이터 안정화
stock['Close_diff2'] = stock['Close_diff1'].diff()
# 3차 차분을 통한 데이터 안정화
stock['Close_diff3'] = stock['Close_diff2'].diff()
# 4차 차분을 통한 데이터 안정화
stock['Close_diff4'] = stock['Close_diff3'].diff()
# 5차 차분을 통한 데이터 안정화
stock['Close_diff5'] = stock['Close_diff4'].diff()
# 원본 데이터, 1차 차분, 2차 차분, 3차 차분, 4차 차분, 5차 차분 데이터 시각화
plt.figure(figsize=(12, 15))
# 원본 데이터 시각화
plt.subplot(6, 1, 1)
plt.plot(stock.index, stock['Close'], label='Original')
plt.title('Original Data')
plt.legend()
# 1차 차분된 데이터 시각화 (NaN을 제외한 부분)
plt.subplot(6, 1, 2)
plt.plot(stock.index[1:], stock['Close_diff1'].dropna(), label='1st Order Differenced', color='orange')
plt.title('1st Order Differenced Data')
plt.legend()
# 2차 차분된 데이터 시각화 (NaN을 제외한 부분)
plt.subplot(6, 1, 3)
plt.plot(stock.index[2:], stock['Close_diff2'].dropna(), label='2nd Order Differenced', color='green')
plt.title('2nd Order Differenced Data')
plt.legend()
# 3차 차분된 데이터 시각화 (NaN을 제외한 부분)
plt.subplot(6, 1, 4)
plt.plot(stock.index[3:], stock['Close_diff3'].dropna(), label='3rd Order Differenced', color='red')
plt.title('3rd Order Differenced Data')
plt.legend()
# 4차 차분된 데이터 시각화 (NaN을 제외한 부분)
plt.subplot(6, 1, 5)
plt.plot(stock.index[4:], stock['Close_diff4'].dropna(), label='4th Order Differenced', color='purple')
plt.title('4th Order Differenced Data')
plt.legend()
# 5차 차분된 데이터 시각화 (NaN을 제외한 부분)
plt.subplot(6, 1, 6)
plt.plot(stock.index[5:], stock['Close_diff5'].dropna(), label='5th Order Differenced', color='brown')
plt.title('5th Order Differenced Data')
plt.legend()
plt.tight_layout()
plt.show()
- 차분을 통해 데이터의 비정상성을 제거하고 변동성을 일정하게 만들며, 이는 시계열 모델링의 성능 향상에 도움을 준다.
- 차분의 차수가 높아질수록 데이터의 추세와 계절성이 더욱 제거되며, 변동성이 감소하지만과도한 차분은 데이터의 의미를 상실하게 만들 수 있으므로, 적절한 차분 선택이 필요하다.
# 2차 차분을 통한 데이터 안정화
stock['Close_diff2'] = stock['Close'].diff().diff()
# NaN 값 제거
diff2_data = stock['Close_diff2'].dropna()
# ACF 및 PACF 플롯 생성
plt.figure(figsize=(12, 6))
plt.subplot(1, 2, 1)
plot_acf(diff2_data, lags=20, ax=plt.gca())
plt.title('ACF of 2nd Order Differenced Data')
plt.subplot(1, 2, 2)
plot_pacf(diff2_data, lags=20, ax=plt.gca())
plt.title('PACF of 2nd Order Differenced Data')
plt.tight_layout()
plt.show()
p와 q 선정 과정
1. ACF 플롯을 통해 q 값 선정
- ACF 플롯을 살펴보면, 특정 시차에서의 상관관계가 급격히 감소하는 지점을 찾는다.
- Cut-off: ACF 플롯에서 특정 시차(lag)에서 상관계수가 유의미하게 0에 가까워지는 지점을 찾는다. 이 지점을 q 값으로 설정한다.
- 예를 들어, ACF 플롯에서 lag 1에서 상관계수가 급격히 감소하고 이후의 값들이 0에 가까워진다면, q = 1로 설정할 수 있다.
2. PACF 플롯을 통해 p 값 선정
- PACF 플롯을 살펴보면, 특정 시차에서의 순수한 상관관계가 급격히 감소하는 지점을 찾는다.
- Cut-off: PACF 플롯에서 특정 시차(lag)에서 상관계수가 유의미하게 0에 가까워지는 지점을 찾는다. 이 지점을 p 값으로 설정한다.
- 예를 들어, PACF 플롯에서 lag 1에서 상관계수가 급격히 감소하고 이후의 값들이 0에 가까워진다면, p = 1로 설정할 수 있다.
# ARIMA 모델 훈련
# p와 q는 ACF와 PACF 플롯을 참고하여 선택합니다. 예를 들어 p=1, q=1로 선택합니다.
model = ARIMA(stock['Close'], order=(1, 2, 1))
model_fit = model.fit()
# 모델 요약
print(model_fit.summary())
# 모델 잔차 분석
residuals = model_fit.resid
plt.figure(figsize=(12, 6))
plt.plot(residuals)
plt.title('Residuals of ARIMA Model')
plt.show()

모델 정보
- 모델: ARIMA(1, 2, 1)
- (1, 2, 1): ARIMA 모델의 파라미터 (p,d,q)(p, d, q)
- p=1p = 1: 자기회귀 차수
- d=2d = 2: 차분 차수
- q=1q = 1: 이동 평균 차수
- (1, 2, 1): ARIMA 모델의 파라미터 (p,d,q)(p, d, q)
모델 적합도 지표
- Log Likelihood: -139.328
- 로그 가능도 값은 모델의 적합도를 나타냅니다. 값이 높을수록 모델이 데이터를 더 잘 설명한다.
- AIC (Akaike Information Criterion): 284.656
- AIC 값이 낮을수록 모델이 데이터에 더 잘 맞음을 나타낸다.
- BIC (Bayesian Information Criterion): 292.411
- BIC 값도 낮을수록 모델의 적합도가 높음을 의미한다.
- HQIC (Hannan-Quinn Information Criterion): 287.793
- HQIC 값도 모델 선택 기준 중 하나로, 낮을수록 좋다.
잔차 분석
- Ljung-Box (L1) (Q): 0.00 (잔차의 자기상관성 검정)
- Prob(Q): 0.96 (p-값이 0.05보다 크므로 잔차가 백색 잡음임을 의미)
- Jarque-Bera (JB): 0.24 (잔차의 정규성 검정)
- Prob(JB): 0.88 (p-값이 0.05보다 크므로 잔차가 정규 분포를 따름)
- Heteroskedasticity (H): 0.66 (이분산성 검정)
- Prob(H): 0.25 (p-값이 0.05보다 커서 이분산성이 없음을 의미)
- Skew: -0.12 (잔차의 왜도)
- Kurtosis: 3.00 (잔차의 첨도)
요약 및 인사이트
- 모델 적합도:
- AIC, BIC, HQIC 값이 비교적 낮아 모델이 데이터를 잘 설명하고 있음을 의미한다.
- 로그 가능도(Log Likelihood) 값도 모델의 적합도를 평가하는 중요한 지표이다.
- 계수의 유의성:
- ar.L1 계수는 p-값이 0.740으로 유의미하지 않음을 나타낸다. 이는 이 계수가 모델에서 중요한 역할을 하지 않을 수 있음을 시사한다.
- ma.L1 계수는 p-값이 0.000으로 매우 유의미하다. 이는 이동 평균 항이 모델에서 중요한 역할을 한다는 것을 나타낸다.
- 잔차 분석:
- Ljung-Box 테스트: p-값이 0.96으로 잔차가 백색 잡음임을 나타낸다. 이는 모델이 데이터를 잘 설명하고 있으며, 잔차에 자기상관성이 없음을 의미한다.
- Jarque-Bera 테스트: p-값이 0.88로 잔차가 정규 분포를 따름을 나타낸다. 이는 잔차가 정규성을 가지며, 모델이 적절하게 데이터를 설명하고 있음을 의미한다.
- Heteroskedasticity 테스트: p-값이 0.25로 잔차가 등분산성을 가짐을 나타낸다. 이는 잔차의 분산이 일정함을 의미한다.

# 미래 예측
forecast = model_fit.forecast(steps=10)
print(forecast)
# 시각화
plt.figure(figsize=(12, 6))
plt.plot(stock.index, stock['Close'], label='Actual')
plt.plot(forecast.index, forecast, label='Forecast', linestyle='--', color='red')
plt.axvline(x=stock.index[-1], color='grey', linestyle='--') # 현재와 미래의 경계선
plt.title('ARIMA Model Forecast')
plt.xlabel('Date')
plt.ylabel('Price')
plt.legend()
plt.show()2021-04-11 6.386569
2021-04-12 6.792197
2021-04-13 7.197831
2021-04-14 7.603464
2021-04-15 8.009098
2021-04-16 8.414731
2021-04-17 8.820365
2021-04-18 9.225998
2021-04-19 9.631632
2021-04-20 10.037265
Freq: D, Name: predicted_mean, dtype: float64
[REFERENCE]
https://www.kaggle.com/competitions/store-sales-time-series-forecasting
Store Sales - Time Series Forecasting | Kaggle
www.kaggle.com
https://ttrhtt12.tistory.com/57
[linear regression]regularization - ridge/lasso
ttrhtt12.tistory.com
https://datalabbit.tistory.com/109
[시계열분석] 백색잡음과정(White Noise Process)
Review 참고 포스팅 : 2021.07.04 - [Statistics/Time Series Analysis] - [시계열분석] 정상성(Stationarity) [시계열분석] 정상성(Stationarity) Review 참고 포스팅 : 2021.02.02 - [Statistics/Time Series Analysis] - [시계열분석] 확
datalabbit.tistory.com
04) FinanceDataReader
FinanceDataReader는 한국 주식 가격, 미국 주식 가격, 지수, 환율, 암호 화폐 가격, 종목 리스트 등을 제공하는 API 패키지입니다. 우선 해당 패키지를 설치해줍…
wikidocs.net
https://ineed-coffee.github.io/posts/Ensemble-concept/#idx1
Ensemble 개념 정리
:mag: Index
ineed-coffee.github.io
https://scikit-learn.org/stable/modules/generated/sklearn.preprocessing.PowerTransformer.html
PowerTransformer
Gallery examples: Compare the effect of different scalers on data with outliers Map data to a normal distribution
scikit-learn.org
강의 01 정규 분포로 분포 변환 (PowerTransformer, 로그 변환)
[https://scikit-learn.org/stable/modules/preprocessing.html#mapping-to-a-gaussian-distribution](htt…
wikidocs.net
https://inhovation97.tistory.com/54
1. Finance Data Reader로 주식 데이터 불러오기 ( 주가 예측 프로젝트 )
학부 연구생으로서 진행한 주가 예측 프로그램의 일련의 과정을 차례로 포스팅합니다. 위 그림처럼 어떤 종목이든 10일간의 데이터로 다음날 종가 상승 여부를 예측하는 머신러닝 프로젝트입니
inhovation97.tistory.com
https://today-1.tistory.com/56
시계열 데이터 전처리(Denoising Method)
시계열 데이터를 분석하는 과정에서 시간 흐름에 따라 변동이 크거나 일정하지 않을 경우 비정상성(Non-Stationarity)을 지니게 되고 이를 전처리 없이 머신러닝 알고리즘에 학습할 경우 단순 후행
today-1.tistory.com
https://velog.io/@dankj1991/time-series-1-Intro
[시계열 머신러닝] 1. 통계 기초 및 시계열 데이터 분석 개요
시계열 데이터 분석에 필요한 개념들을 정리하는 시리즈 - 1. 통계 기초 및 시계열 데이터 분석 개요 편
velog.io
https://velog.io/@phs5145/%EC%8B%9C%EA%B3%84%EC%97%B4-%EB%8D%B0%EC%9D%B4%ED%84%B0-Time-series
시계열 데이터 Time-series
시계열이란 일정 시간 간격으로 배치된 데이터들의 수열을 말합니다. 즉, 시간의 흐름이 포함되어 있는 데이터라고 볼 수 있겠습니다.위와 같이 계절성, 추세가 있는 시계열이 있고 없는 시계열
velog.io
'데이터분석' 카테고리의 다른 글
| 시계열 데이터 분석 (1) | 2024.07.07 |
|---|---|
| ClumnTransformer (0) | 2024.05.08 |
| 서울 법정동(자치구) 코드북 (0) | 2024.01.30 |
| melt(데이터프레임 변형) 개념 및 예제 (0) | 2024.01.19 |
| linear regression(ridge & lasso) coding implementation (0) | 2023.11.22 |